搜索
【题目】如图，
与
都是等边三角形，
、
、
三边长是一组勾股数，且边最长．
（1）求证：
（2）求
的度数．
参考答案：
【答案】（1）见解析，（2）∠ADB=150°．
【解析】
（1）由“SAS”可证△ABD≌△CBE，可得AD=EC，∠ADB=∠BEC，由勾股数可得结论； （2）由勾股定理的逆定理可得∠DEC=90°，由全等三角形的性质可求解．
证明：（1）∵△ABC与△DBE都是等边三角形，
∴AB=BC，BD=DE=BE，∠ABC=∠DBE
60°，
∴∠ABD=∠CBE，且AB=BC，DB=BE，
∴△ABD≌△CBE（SAS）
∴AD=EC，∠ADB=∠BEC，
∵DA、DB、DC三边长是一组勾股数，且DC边最长．
∴
∴
（2）∵
，
∴∠DEC=90°，
∴∠BEC=
150°
∴∠ADB=∠BEC=150°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为
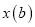，两车之间的距离为
，图中的折线表示
与
之间的关系，下列说法中正确的个数为（ ）.①甲乙两地相距
；②
段表示慢车先加速后减速最后到达甲地；③快车的速度为
；④慢车的速度为
；⑤快车到达乙地
后，慢车到达甲地。
A.
个B. 
个C. 
个D. 
个 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC为锐角三角形，AD是BC边上的高，正方形EFGH的一边FG在BC上，顶点E、H分别在AB、AC上，已知BC=40cm，AD=30cm．
（1）求证：△AEH∽△ABC；
（2）求这个正方形的边长与面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在
中，
，
，
的平分线与
的垂直平分线交于点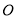
，点
沿
折叠后与点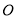重合，则
的度数是__________度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】近年来多肉植物风靡全国．花农王大伯分别培植了一批国产多肉与进口多肉．第一次出售国产多肉与进口多肉各100盆，售后发现：国产多肉的平均每盆利润是5元并且始终不变；进口多肉的平均每盆利润是15元，每增加1盆，进口多肉的平均每盆利润增加1元．王大伯计划第二次出售国产多肉与进口多肉共200盆，设进口多肉比第一次增加x盆．
（1）用含x的代数式分别表示第二次国产多肉与进口多肉售完后的利润；
（2）要使第二次国产多肉与进口多肉售完后的总利润比第一次国产多肉与进口多肉售完后总利润多60%，求此时x的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
，
，C、B、D在同一条直线上．
（1）若
，
，连接
，求的长．（2）如图设a、b、c是
和
的边长，这时我们把关于x的形如
的一元二次方程称为“勾股方程”．①写出一个“勾股方程”；
②判断关于x的“勾股方程”
根的情况并说明理由；③若
是“勾股方程”的一个根，且四边形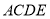
的周长是
，求
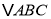的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，⊙O 的直径AB=2,AM和BN是它的两条切线，DE切⊙O于E，交AM于D，交BN于C．设
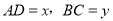．（1）求证：
；（2）求
关于
的关系式.
相关试题
