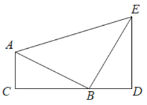
【题目】如图,![]() ,
,![]() ,C、B、D在同一条直线上.
,C、B、D在同一条直线上.

(1)若![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 的长.
的长.
(2)如图设a、b、c是![]() 和
和![]() 的边长,这时我们把关于x的形如
的边长,这时我们把关于x的形如![]() 的一元二次方程称为“勾股方程”.
的一元二次方程称为“勾股方程”.
①写出一个“勾股方程”;
②判断关于x的“勾股方程”![]() 根的情况并说明理由;
根的情况并说明理由;
③若![]() 是“勾股方程”
是“勾股方程”![]() 的一个根,且四边形
的一个根,且四边形![]() 的周长是
的周长是![]() ,求
,求![]() 的面积.
的面积.

参考答案:
【答案】(1)![]() (2)①
(2)①![]() ②关于x的“勾股方程”
②关于x的“勾股方程”![]() 必有实数根,理由见解析.③
必有实数根,理由见解析.③![]()
【解析】
(1)由Rt△ABC≌Rt△BED,知BD=AC=1,DE=BC=![]() ∠ABC=∠BED,∠BAC=∠EBD,再证AB=BE=
∠ABC=∠BED,∠BAC=∠EBD,再证AB=BE=![]() ,∠ABE=90°,利用勾股定理可得答案;
,∠ABE=90°,利用勾股定理可得答案;
(2)①直接找一组勾股数代入方程即可;②通过判断根的判别式△的正负来证明结论;③利用根的意义和勾股定理作为相等关系先求得c的值,根据完全平方公式求得ab的值,从而可求得面积.
解:(1)∵Rt△ABC≌Rt△BED,
∴BD=AC=1,DE=BC=![]() ∠ABC=∠BED,∠BAC=∠EBD,
∠ABC=∠BED,∠BAC=∠EBD,
∴AB=BE=![]() ,
,
∵∠ABC+∠BAC=90°,
∴∠ABC+∠EBD=90°,
∴∠ABE=90°,
∴AE= ![]()
(2)①当a=3,b=4,c=5时,勾股方程为为![]()
②关于x的“勾股方程”![]() 必有实数根,
必有实数根,
理由如下:根据题意,得:![]()
∵![]()
∴![]()
即△≥0,
∴勾股方程![]() 必有实数根;
必有实数根;
③当![]() 时,有
时,有![]()
即![]()
∵四边形![]() 的周长是
的周长是![]() ,
,
![]()
![]() 即
即![]()
∴![]()
∴c=3,
∴![]()
![]()
∵![]()
![]()
∴![]()
∴![]() =
=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,
, 的平分线与
的平分线与 的垂直平分线交于点
的垂直平分线交于点 ,点
,点 沿
沿 折叠后与点
折叠后与点 重合,则
重合,则 的度数是__________度.
的度数是__________度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 与
与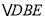 都是等边三角形,
都是等边三角形, 、
、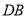 、
、 三边长是一组勾股数,且
三边长是一组勾股数,且 边最长.
边最长.
(1)求证:

(2)求
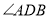 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】近年来多肉植物风靡全国.花农王大伯分别培植了一批国产多肉与进口多肉.第一次出售国产多肉与进口多肉各100盆,售后发现:国产多肉的平均每盆利润是5元并且始终不变;进口多肉的平均每盆利润是15元,每增加1盆,进口多肉的平均每盆利润增加1元.王大伯计划第二次出售国产多肉与进口多肉共200盆,设进口多肉比第一次增加x盆.
(1)用含x的代数式分别表示第二次国产多肉与进口多肉售完后的利润;
(2)要使第二次国产多肉与进口多肉售完后的总利润比第一次国产多肉与进口多肉售完后总利润多60%,求此时x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O 的直径AB=2,AM和BN是它的两条切线,DE切⊙O于E,交AM于D,交BN于C.设
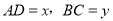 .
.(1)求证:
 ;(2)求
;(2)求 关于
关于 的关系式.
的关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是
 的的直径,BC
的的直径,BC AB于点B,连接OC交
AB于点B,连接OC交 于点E,弦AD//OC,弦DF
于点E,弦AD//OC,弦DF AB于点G.
AB于点G.(1)求证:点E是
 的中点;
的中点;(2)求证:CD是
 的切线;
的切线;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,AB=26,AD=6,将□ABCD绕点A旋转,当点D的对应点D′落在AB边上时,点C的对应点C′恰好与点B、C在同一直线上,则此时△C′D′B的面积为()

A.120B.240C.260D.480
相关试题

