【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直于x轴、垂足为点B,反比例函数y= ![]() (x<0)的图象经过AO的中点C、且与AB相交于点D,OB=8、AD=6.
(x<0)的图象经过AO的中点C、且与AB相交于点D,OB=8、AD=6. 
(1)求反比例函数y= ![]() 的解析.
的解析.
(2)求经过C,D两点的一次函数解析式.
参考答案:
【答案】
(1)解:设点D的坐标为(8,m)(m>0),则点A的坐标为(8,6+m),
∵点C为线段AO的中点,
∴点C的坐标为(4, ![]() ).
).
∵点C、点D均在反比例函数y= ![]() 的函数图象上,
的函数图象上,
∴ ![]() ,解得:
,解得: ![]()
(2)∵m=2,
∴点C的坐标为(4,4),点D的坐标为(8,6).
设经过点C、D的一次函数的解析式为y=ax+b,
则有 ![]() ,解得:
,解得: ![]() .
.
∴经过C、D两点的一次函数解析式为y=﹣ ![]() x+2
x+2
【解析】(1)设点D的坐标为(8,m)(m>0),则点A的坐标为(8,6+m),由点A的坐标表示出点C的坐标,根据C、D点在反比例函数图象上结合反比例函数图象上点的坐标特征即可得出关于k、m的二元一次方程,解方程即可得出结论;(2)由m的值,可找出点C、D的坐标,设出过点C、D的一次函数的解析式为y=ax+b,由点C、D的坐标利用待定系数法即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示);若不改变,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】从一副扑克牌中取出方块3、红心6、黑挑10共三张牌,洗匀后正面朝下放在桌面上,小明和小丽玩摸牌游戏,游戏规则如下:先由小明随机摸出一张牌,记下牌面数字后放回,洗匀后正面朝下,再由小丽随机摸出一张牌,记下牌面数字、这样记为一次游戏.当两人摸出的牌面数字不同时,牌面数字大的获胜;当两人摸出的牌面数字相同,则为平局.

(1)用画树状图或列表法,列出小明、小丽两人一次游戏的所有可能的结果.
(2)求小明获胜的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1为放置在水平桌面上的某创意可折叠台灯的平面示意图,将其抽象成图2,量的∠DCB=60°,∠CDE=150°,灯杆CD的长为40cm,灯管DE的长为26cm,底座AB的厚度为2cm,不考虑其他因素,分别求出DE与水平卓,面(AB所在的直线)所成的夹角度数和台灯的高(点E到桌面的距离).(结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】张庄甲、乙两家草莓采摘园的草莓销售价格相同,“春节期间”,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为
 (千克),在甲园所需总费用为
(千克),在甲园所需总费用为 (元),在乙园所需总费用为
(元),在乙园所需总费用为 (元),
(元), 、
、 与
与 之间的函数关系如图所示,折线OAB表示
之间的函数关系如图所示,折线OAB表示 与
与 之间的函数关系.
之间的函数关系.
(1)甲采摘园的门票是 元,两个采摘园优惠前的草莓单价是每千克 元;
(2)当
 >10时,求
>10时,求 与
与 的函数表达式;
的函数表达式;(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图书管理员小张要骑车从学校到教育局,一出校门,遇到了王老师,王老师说:“今天有风,而且去时逆风,要吃亏了”,小张回答说:“去时逆风,回来时顺风,和无风往返一趟所用时间相同”.(顺风速度=无风时骑车速度+风速,逆风速度=无风时骑车速度-风速)
(1)如果学校到教育局的路程是15 km,无风时小张骑自行车的速度是20 km/h,他逆风去教育局所用时间是顺风回学校所用时间的
 倍,求风速是多少?
倍,求风速是多少?(2)如果设从学校到教育局的路程为s千米,无风时骑车速度为v千米/时,风速为a千米/时(v>a),那么有风往返一趟的时间 无风往返一趟的时间(填“>”、“<”或“=”),试说明理由.
-
科目: 来源: 题型:
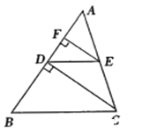
查看答案和解析>>【题目】如图,CD⊥AB于D,EF⊥AB于F.
(1)求证:EF∥CD;
(2)若DE∥BC,EF平分∠AED,求证:CD平分∠ACB.
相关试题

