【题目】图书管理员小张要骑车从学校到教育局,一出校门,遇到了王老师,王老师说:“今天有风,而且去时逆风,要吃亏了”,小张回答说:“去时逆风,回来时顺风,和无风往返一趟所用时间相同”.(顺风速度=无风时骑车速度+风速,逆风速度=无风时骑车速度-风速)
(1)如果学校到教育局的路程是15 km,无风时小张骑自行车的速度是20 km/h,他逆风去教育局所用时间是顺风回学校所用时间的![]() 倍,求风速是多少?
倍,求风速是多少?
(2)如果设从学校到教育局的路程为s千米,无风时骑车速度为v千米/时,风速为a千米/时(v>a),那么有风往返一趟的时间 无风往返一趟的时间(填“>”、“<”或“=”),试说明理由.
参考答案:
【答案】(1)当天的风速为5 km/h;(2)>,理由详见解析.
【解析】
(1)首先设当天的风速为x km/h,则顺风的速度为(20+x)千米/时,逆风速度是(20-x)千米/时,根据逆风去教育局所用时间是顺风回学校所用时间的![]() 倍列出方程即可;
倍列出方程即可;
(2)无风时的时间=总路程÷无风时的速度;有风时的时间=单程的路程÷顺风的速度+单程的路程÷逆风的速度,进而让两个代数式相减,根据作差比较法可知结论.
解:(1)设当天的风速为x km/h.根据题意,得
![]() =
=![]() .
.
解这个方程,得x=5.
经检验,x=5是所列方程的解.
答:当天的风速为5 km/h.
(2)>,理由如下:
有风往返一趟的时间为(![]() )小时,无风往返一趟的时间为
)小时,无风往返一趟的时间为![]() 小时.
小时.
∵![]() -
-![]() =
=![]() ,
,
又∵v>a,
∴![]() >0,即
>0,即![]() >
>![]() .
.
∴有风往返一趟的时间>无风往返一趟的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1为放置在水平桌面上的某创意可折叠台灯的平面示意图,将其抽象成图2,量的∠DCB=60°,∠CDE=150°,灯杆CD的长为40cm,灯管DE的长为26cm,底座AB的厚度为2cm,不考虑其他因素,分别求出DE与水平卓,面(AB所在的直线)所成的夹角度数和台灯的高(点E到桌面的距离).(结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直于x轴、垂足为点B,反比例函数y=
 (x<0)的图象经过AO的中点C、且与AB相交于点D,OB=8、AD=6.
(x<0)的图象经过AO的中点C、且与AB相交于点D,OB=8、AD=6. 
(1)求反比例函数y= 的解析.
的解析.
(2)求经过C,D两点的一次函数解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】张庄甲、乙两家草莓采摘园的草莓销售价格相同,“春节期间”,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为
 (千克),在甲园所需总费用为
(千克),在甲园所需总费用为 (元),在乙园所需总费用为
(元),在乙园所需总费用为 (元),
(元), 、
、 与
与 之间的函数关系如图所示,折线OAB表示
之间的函数关系如图所示,折线OAB表示 与
与 之间的函数关系.
之间的函数关系.
(1)甲采摘园的门票是 元,两个采摘园优惠前的草莓单价是每千克 元;
(2)当
 >10时,求
>10时,求 与
与 的函数表达式;
的函数表达式;(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
-
科目: 来源: 题型:
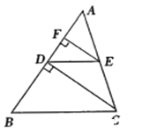
查看答案和解析>>【题目】如图,CD⊥AB于D,EF⊥AB于F.
(1)求证:EF∥CD;
(2)若DE∥BC,EF平分∠AED,求证:CD平分∠ACB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径AD长为6,AB是弦,∠A=30°,CD∥AB,且CD=
 .
. 
(1)求∠C的度数;
(2)求证:BC是⊙O的切线;
(3)求阴影部分面积.
相关试题

