【题目】在平面直角坐标系中,如图1,将线段AB平移至线段CD,连接AC、BD.

(1)已知A(﹣3,0)、B(﹣2,﹣2),点C在y轴的正半轴上,点D在第一象限内,且三角形ACO的面积是6,求点C、D的坐标;
(2)如图2,在平面直角坐标系中,已知一定点M(1,0),两个动点E(a,2a+1)、F(b,﹣2b+3).
①请你探索是否存在以两个动点E、F为端点的线段EF平行于线段OM且等于线段OM,若存在,求出点E、F两点的坐标;若不存在,请说明理由;
②当点E、F重合时,将该重合点记为点P,另当过点E、F的直线平行于x轴时,是否存在△PEF的面积为2?若存在,求出点E、F两点的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)C的坐标为(0,4),点D的坐标为(1,2);(2)①点E的坐标为(1,3),F的坐标为(0,3)或点E的坐标为(0,1),F的坐标为(1,1);②存在△PEF的面积为2,点E、F两点的坐标为E(﹣![]() ,0)、F(
,0)、F(![]() ,0),或E(
,0),或E(![]() ,4)、F(﹣
,4)、F(﹣![]() ,4).
,4).
【解析】
(1)由点A和点C在y轴上确定出向右平移3个单位,再根据△ACD的面积求出向上平移的单位,然后写出点C、D的坐标即可.
(2)①根据线段EF平行于线段OM且等于线段OM,得出2a+1=﹣2b+3,|a﹣b|=1,解答即可;
②首先根据题意求出点P的坐标为(![]() ,2),设点E在F的左边,由EF∥x轴得出a+b=1,求出△PEF的面积=
,2),设点E在F的左边,由EF∥x轴得出a+b=1,求出△PEF的面积=![]() (b﹣a)×|2a+1﹣2|=2,得出(b﹣a)|2a﹣1|=4,当EF在点P的上方时,(b﹣a)(2a﹣1)=4,与a+b=1联立得:
(b﹣a)×|2a+1﹣2|=2,得出(b﹣a)|2a﹣1|=4,当EF在点P的上方时,(b﹣a)(2a﹣1)=4,与a+b=1联立得:![]() ,此方程组无解;当EF在点P的下方时,(b﹣a)(1﹣2a)=4,与a+b=1联立得:
,此方程组无解;当EF在点P的下方时,(b﹣a)(1﹣2a)=4,与a+b=1联立得:![]() ,解得:
,解得: ,或
,或 ;分别代入点E(a,2a+1)、F(b,﹣2b+3)即可.
;分别代入点E(a,2a+1)、F(b,﹣2b+3)即可.
解:(1)∵A(﹣3,0),点C在y轴的正半轴上,
∴向右平移3个单位,
设向上平移x个单位,
∵S△ACO=![]() OA×OC=6,
OA×OC=6,
∴![]() ×3x=6,
×3x=6,
解得:x=4,
∴点C的坐标为(0,4),
﹣2+3=1,﹣2+4=2,
故点D的坐标为(1,2).
(2)①存在;理由如下:
∵线段EF平行于线段OM且等于线段OM,
∴2a+1=﹣2b+3,|a﹣b|=1,
解得:a=1,b=0或a=0,b=1,
即点E的坐标为(1,3),F的坐标为(0,3)或点E的坐标为(0,1),F的坐标为(1,1);
②存在,理由如下:如图2所示:
当点E、F重合时,![]() ,
,
解得:![]() ,
,
∴2a+1=2,
∴点P的坐标为(![]() ,2),
,2),
设点E在F的左边,
∵EF∥x轴,
∴2a+1=﹣2b+3,
∴a+b=1,
∵△PEF的面积=![]() (b﹣a)×|2a+1﹣2|=2,
(b﹣a)×|2a+1﹣2|=2,
即(b﹣a)|2a﹣1|=4,
当EF在点P的上方时,(b﹣a)(2a﹣1)=4,与a+b=1联立得:![]() ,此方程组无解;
,此方程组无解;
当EF在点P的下方时,(b﹣a)(1﹣2a)=4,与a+![]() =1联立得:
=1联立得:![]() ,
,
解得: ,或
,或 ;
;
分别代入点E(a,2a+1)、F(b,﹣2b+3)得:E(﹣![]() ,0)、F(
,0)、F(![]() ,0),或E(
,0),或E(![]() ,4)、F(﹣
,4)、F(﹣![]() ,4);
,4);
综上所述,存在△PEF的面积为2,点E、F两点的坐标为E(﹣![]() ,0)、F(
,0)、F(![]() ,0),或E(
,0),或E(![]() ,4)、F(﹣
,4)、F(﹣![]() ,4).
,4).

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校课外兴趣小组在本校学生中开展“感动中国2014年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
类别
A
B
C
D
频数
30
40
24
b
频率
a
0.4
0.24
0.06

(1)表中的a=________,b=________;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c (a、b、c为常数且a≠0)中的x与y的部分对应值如下表,
x
…
-3
-2
-1
0
1
2
3
4
5
…
y
…
12
5
0
-3
-4
-3
0
5
12
…
下列四个结论:
(1)二次函数y=ax2+bx+c 有最小值,最小值为-3;
(2)抛物线与y轴交点为(0,-3);
(3)二次函数y=ax2+bx+c 的图像对称轴是x=1;
(4)本题条件下,一元二次方程ax2+bx+c的解是x1=-1,x2=3.
其中正确结论的个数是( )
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是直角三角形,延长AB到点E,使BE=BC,在BC上取一点F,使BF=AB,连接EF.△ABC旋转后能与△FBE重合,请回答:
(1)旋转中心是点____,
(2)旋转了____度,
(3) AC与EF的关系为_________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明晚饭后外出散步,遇见同学,交谈一会,返回途中在读报厅看了一会报.下图是根据此情景画出的图象,请你回答下列问题:
(1)小明在距家多远遇见同学的,交谈了多少时间?
(2)读报厅离家多远?
(3)小明在哪一段路程中走得最快,速度是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(4,3)是反比例函数y=
 在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=
在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y= 的图象于点P.
的图象于点P.(1)求反比例函数y=
 的表达式;
的表达式;(2)求点B的坐标;
(3)求△OAP的面积.

-
科目: 来源: 题型:
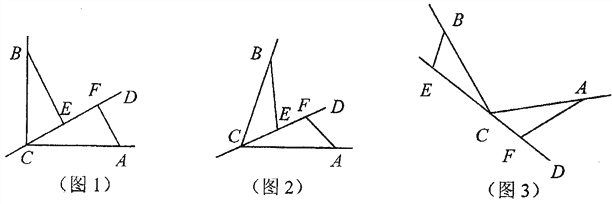
查看答案和解析>>【题目】已知CD是经过∠BCA顶点C的一条直线,CA=CB.E、F分别是直线CD上两点,且∠BEC=∠CFA=∠
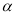 .
.
(1)若直线CD经过∠BCA的内部,且E、F在射线CD上,请解决下面问题:
①如图1若∠BCA=90°,∠
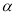 =90°、探索三条线段EF、BE、AF的数量关系并证明你的结论.
=90°、探索三条线段EF、BE、AF的数量关系并证明你的结论.②如图2,若0°<∠BCA<180°, 请添加一个关于∠
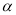 与∠BCA关系的条件___ ____使①中的结论仍然成立;
与∠BCA关系的条件___ ____使①中的结论仍然成立;(2)如图3,若直线CD经过∠BCA的外部,∠
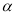 =∠BCA,请写出三条线段EF、BE、AF的数量关系并证明你的结论.
=∠BCA,请写出三条线段EF、BE、AF的数量关系并证明你的结论.
相关试题

