【题目】已知CD是经过∠BCA顶点C的一条直线,CA=CB.E、F分别是直线CD上两点,且∠BEC=∠CFA=∠![]() .
.
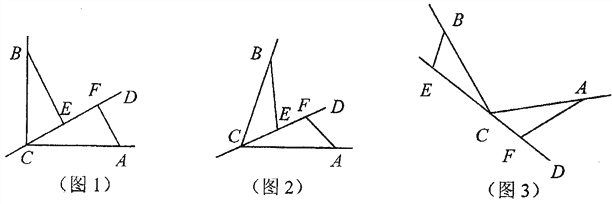
(1)若直线CD经过∠BCA的内部,且E、F在射线CD上,请解决下面问题:
①如图1若∠BCA=90°,∠![]() =90°、探索三条线段EF、BE、AF的数量关系并证明你的结论.
=90°、探索三条线段EF、BE、AF的数量关系并证明你的结论.
②如图2,若0°<∠BCA<180°, 请添加一个关于∠![]() 与∠BCA关系的条件___ ____使①中的结论仍然成立;
与∠BCA关系的条件___ ____使①中的结论仍然成立;
(2)如图3,若直线CD经过∠BCA的外部,∠![]() =∠BCA,请写出三条线段EF、BE、AF的数量关系并证明你的结论.
=∠BCA,请写出三条线段EF、BE、AF的数量关系并证明你的结论.
参考答案:
【答案】(1)①EF、BE、AF的数量关系: ![]() (相关等式均可,证明详见解析; ②∠
(相关等式均可,证明详见解析; ②∠![]() 与∠BCA关系:∠
与∠BCA关系:∠ ![]() +∠BCA=180°(或互补,相关等式均可);(2)EF、BE、AF的数量关系:
+∠BCA=180°(或互补,相关等式均可);(2)EF、BE、AF的数量关系: ![]() (相关等式均可) ,证明详见解析.
(相关等式均可) ,证明详见解析.
【解析】试题分析:(1)①求出∠BEC=∠AFC=90°,∠CBE=∠ACF,根据AAS证△BCE≌△CAF,推出BE=CF,CE=AF即可;.
②求出∠BEC=∠AFC,∠CBE=∠ACF,根据AAS证△BCE≌△CAF,推出BE=CF,CE=AF即可;.
(2)求出∠BEC=∠AFC,∠CBE=∠ACF,根据AAS证△BCE≌△CAF,推出BE=CF,CE=AF即可.
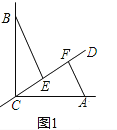
试题解析:(1)①如图1中,.
 .
.
E点在F点的左侧,.
∵BE⊥CD,AF⊥CD,∠ACB=90°,.
∴∠BEC=∠AFC=90°,.
∴∠BCE+∠ACF=90°,∠CBE+∠BCE=90°,.
∴∠CBE=∠ACF,.
在△BCE和△CAF中,.
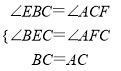 ,.
,.
∴△BCE≌△CAF(AAS),.
∴BE=CF,CE=AF,.
∴EF=CF-CE=BE-AF,.
当E在F的右侧时,同理可证EF=AF-BE,.
∴EF=|BE-AF|;
②∠α+∠ACB=180°时,①中两个结论仍然成立;.
证明:如图2中,.
 .
.
∵∠BEC=∠CFA=∠a,∠α+∠ACB=180°,.
∴∠CBE=∠ACF,.
在△BCE和△CAF中,.
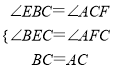 ,.
,.
∴△BCE≌△CAF(AAS),.
∴BE=CF,CE=AF,.
∴EF=CF-CE=BE-AF,.
当E在F的右侧时,同理可证EF=AF-BE,.
∴EF=|BE-AF|;
(2)EF=BE+AF..
理由是:如图3中,.
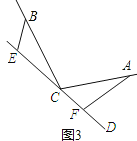 .
.
∵∠BEC=∠CFA=∠a,∠a=∠BCA,.
又∵∠EBC+∠BCE+∠BEC=180°,∠BCE+∠ACF+∠ACB=180°,.
∴∠EBC+∠BCE=∠BCE+∠ACF,.
∴∠EBC=∠ACF,.
在△BEC和△CFA中,.
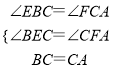 ,.
,.
∴△BEC≌△CFA(AAS),.
∴AF=CE,BE=CF,.
∵EF=CE+CF,.
∴EF=BE+AF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=k1x+b与双曲线y=
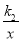 相交于点A(1,2),B(m,-1)两点.
相交于点A(1,2),B(m,-1)两点.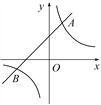
(1)分别求直线和双曲线的表达式;
(2)若A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1,y2,y3的大小关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.
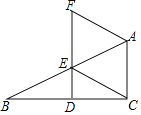
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )

A. (
 ,0) B. (2,0) C. (
,0) B. (2,0) C. ( ,0) D. (3,0)
,0) D. (3,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD中,AD∥BC,AP平分∠DAB,BP平分∠ABC,它们的交点P在线段CD上,下面的结论:①AP⊥BP;②点P到直线AD,BC的距离相等;③PD=PC.其中正确的结论有( )

A. ①②③ B. ①② C. ① D. ②
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个样本,27,23,25,27,29,31,27,30,32,31,28,26,27,29,28,24,26,27,28,30,以2为组距画出频数分布直方图
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2-2x-m2=0.
(1)求证:该方程有两个不相等的实数根;
(2)若该方程有两个实数根为x1,x2,且x1=2x2+5,求m的值.
相关试题

