【题目】如图,E是矩形ABCD的边AD上一点,且BE=ED,P是对角线BD上任一点,PF⊥BE,PG⊥AD,垂足分别为F,G,求证:PF+PG=AB.

参考答案:
【答案】见解析
【解析】
连接EP,用两种方法表示出△BED的面积,S△BED=![]() DE·AB……①,S△BED=S△EDP+S△BEP=
DE·AB……①,S△BED=S△EDP+S△BEP=![]() ED·(PG+PF)……②,然后整理即可得到结论.
ED·(PG+PF)……②,然后整理即可得到结论.
S△BED=![]() DE·AB……①,
DE·AB……①,
连接EP,则S△BED=S△EPD+S△BEP,S△EDP=![]() ED·PG,S△BEP=
ED·PG,S△BEP=![]() BE·PF,
BE·PF,
∵BE=ED,
∴S△BEP=![]() ED·PF,
ED·PF,
∴S△BED=S△EDP+S△BEP=![]() ED·(PG+PF)……②.
ED·(PG+PF)……②.
综合①②可得:![]() DE·AB=
DE·AB=![]() ED·(PG+PF),
ED·(PG+PF),
∴AB=PG+PF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)任意四边形四边中点围成的四边形是__________;
(2)对角线相等的四边形四边中点围成的四边形是__________;
(3)对角线垂直的四边形四边中点围成的四边形是__________;并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△DEB中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是

A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=4,E为BC中点,AE⊥BC于点E,AF⊥CD于点F,CG∥AE,CG交AF于点H,交AD于点G.
(1)求菱形ABCD的面积;(2)求∠CHA的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学活动课中,小辉将边长为
 和3的两个正方形放置在直线l上,如图1,他连结AD、CF,经测量发现AD=CF.
和3的两个正方形放置在直线l上,如图1,他连结AD、CF,经测量发现AD=CF.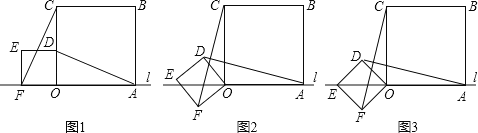
(1)他将正方形ODEF绕O点逆时针旋转一定的角度,如图2,试判断AD与CF还相等吗?说明你的理由;
(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图3,请你求出CF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.

(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的正方形ABCD中,动点P从A点出发,以每秒1个单位长度的速度沿AB向B点运动,同时动点Q从B点出发,以每秒2个单位长度的速度沿BC→CD方向运动,当P运动到B点时,P、Q两点同时停止运动.设P点运动的时间为t,△APQ的面积为S,则S与t的函数关系的图象是【 】

相关试题

