【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.

(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
参考答案:
【答案】(1)见解析(2)成立
【解析】
试题(1)由DF=BE,四边形ABCD为正方形可证△CEB≌△CFD,从而证出CE=CF.
(2)由(1)得,CE=CF,∠BCE+∠ECD=∠DCF+∠ECD即∠ECF=∠BCD=90°又∠GCE=45°所以可
得∠GCE=∠GCF,故可证得△ECG≌△FCG,即EG=FG=GD+DF.又因为DF=BE,所以可证出GE=BE+GD成立.
试题解析:(1)在正方形ABCD中,
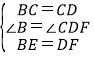
∴△CBE≌△CDF(SAS).
∴CE=CF.
(2)GE=BE+GD成立.
理由是:∵由(1)得:△CBE≌△CDF,
∴∠BCE=∠DCF,
∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,
又∵∠GCE=45°,∴∠GCF=∠GCE=45°. CE=CF
∵∠GCE=∠GCF, GC=GC
∴△ECG≌△FCG(SAS).
∴GE=GF.
∴GE=DF+GD=BE+GD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
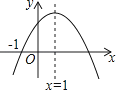
A.a>0
B.c<0
C.3是方程ax2+bx+c=0的一个根
D.当x<1时,y随x的增大而减小 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).

(1)请直接写出点B关于点A对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个小组同时从甲地出发,匀速步行到乙地,甲乙两地相距7500米,第一组的步行速度是第二组的1.2倍,并且比第二组早15分钟到达乙地.设第二组的步行速度为x千米/小时,根据题意可列方程是( )
A.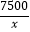 ﹣
﹣ 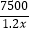 =15
=15
B.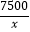 ﹣
﹣ 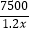 =
= 
C.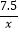 ﹣
﹣ 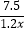 =15
=15
D.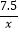 ﹣
﹣ 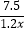 =
= 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】某学生社团为了解本校学生喜欢球类运动的情况,随机抽取了若干名学生进行问卷调查,要求每位学生只能填写一种自己喜欢的球类运动,并将调查的结果绘制成如下的两幅不完整的统计图.
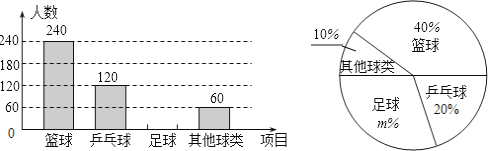
请根据统计图表提供的信息,解答下列问题:
(1)参加调查的人数共有△人;在扇形图中,m=△;将条形图补充完整;
(2)如果该校有3500名学生,则估计喜欢“篮球”的学生共有多少人?
(3)该社团计划从篮球、足球和乒乓球中,随机抽取两种球类组织比赛,请用树状图或列表法,求抽取到的两种球类恰好是“篮球”和“足球”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中
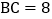 ,
,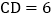 ,将
,将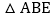 沿BE折叠,使点A恰好落在对角线BD上F处,则DE的长是
沿BE折叠,使点A恰好落在对角线BD上F处,则DE的长是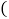
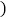

A. 3 B.
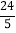 C. 5 D.
C. 5 D. 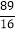
相关试题

