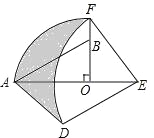
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( )
A.π B.![]() C.3+π D.8﹣π
C.3+π D.8﹣π
参考答案:
【答案】D.
【解析】
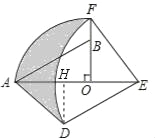
试题分析:作DH⊥AE于H,已知∠AOB=90°,OA=3,OB=2,根据勾股定理求出AB=![]() ,由旋转的性质可知,OE=OB=2,DE=EF=AB=
,由旋转的性质可知,OE=OB=2,DE=EF=AB=![]() ,△DHE≌△BOA,所以DH=OB=2,所以阴影部分面积=△ADE的面积+△EOF的面积+扇形AOF的面积﹣扇形DEF的面积=
,△DHE≌△BOA,所以DH=OB=2,所以阴影部分面积=△ADE的面积+△EOF的面积+扇形AOF的面积﹣扇形DEF的面积=![]() ×5×2+
×5×2+![]() ×2×3+
×2×3+![]() ﹣
﹣![]()
=8﹣π,故答案选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016山西省第22题)综合与实践
问题情境
在综合与实践课上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动,如图1,将一张菱形纸片ABCD(
 )沿对角线AC剪开,得到
)沿对角线AC剪开,得到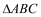 和
和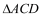 .
.操作发现
(1)将图1中的
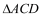 以A为旋转中心,逆时针方向旋转角
以A为旋转中心,逆时针方向旋转角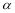 ,使
,使 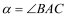 ,得到如图2所示的
,得到如图2所示的 ,分别延长BC 和
,分别延长BC 和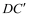 交于点E,则四边形
交于点E,则四边形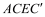 的状是 ;
的状是 ;(2)创新小组将图1中的
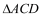 以A为旋转中心,按逆时针方向旋转角
以A为旋转中心,按逆时针方向旋转角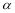 ,使
,使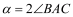 ,得到如图3所
,得到如图3所示的
 ,连接DB,
,连接DB,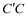 ,得到四边形
,得到四边形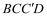 ,发现它是矩形.请你证明这个论;
,发现它是矩形.请你证明这个论;(3)缜密小组在创新小组发现结论的基础上,量得图3中BC=13cm,AC=10cm,然后提出一个问题:将
 沿着射线DB方向平移acm,得到
沿着射线DB方向平移acm,得到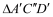 ,连接
,连接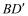 ,
,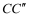 ,使四边形
,使四边形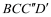 恰好为正方形,求a的值.请你解答此问题;
恰好为正方形,求a的值.请你解答此问题;(4)请你参照以上操作,将图1中的
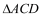 在同一平面内进行一次平移,得到
在同一平面内进行一次平移,得到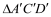 ,在图4中画出平移后构造出的新图形,标明字母,说明平移及构图方法,写出你发现的结论,不必证明.
,在图4中画出平移后构造出的新图形,标明字母,说明平移及构图方法,写出你发现的结论,不必证明.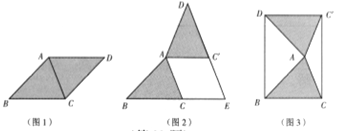
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆锥的轴截面是( )
A.梯形B.等腰三角形C.矩形D.圆
-
科目: 来源: 题型:
查看答案和解析>>【题目】若整式M,N满足式子M+N=x2-3,其中M=3x-3,求N
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC和△DBE均为等腰直角三角形.
(1)求证:AD=CE;
(2)求证:AD和CE垂直.

-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“如果两个角相等,那么它们都是直角”的逆命题是( )
A.如果两个角不相等,那么它们都不是直角
B.如果两个角都不是直角,那么这两个角不相等
C.如果两个角都是直角,那么这两个角相等
D.相等的两个角都是直角 -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程(2x-1)2+n2+1=0的根的情况是( )
A.有两个不相等的实数根B.有两个相等的实数根
C.没有实数根D.无法判定
相关试题

