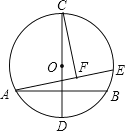
【题目】如图,在半径为4的⊙O中,CD为直径,AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】D
【解析】
连接AC,AO,由AB⊥CD,利用垂径定理得到G为AB的中点,由中点的定义确定出OG的长,在直角三角形AOG中,由AO与OG的长,利用勾股定理求出AG的长,进而确定出AB的长,由CO+GO求出CG的长,在直角三角形AGC中,利用勾股定理求出AC的长,由CF垂直于AE,得到三角形ACF始终为直角三角形,点F的运动轨迹为以AC为直径的半径,如图中红线所示,当E位于点B时,CG⊥AE,此时F与G重合;当E位于D时,CA⊥AE,此时F与A重合,可得出当点E从点B出发顺时针运动到点D时,点F所经过的路径长![]() ,在直角三角形ACG中,利用锐角三角函数定义求出∠ACG的度数,进而确定出
,在直角三角形ACG中,利用锐角三角函数定义求出∠ACG的度数,进而确定出![]() 所对圆心角的度数,再由AC的长求出半径,利用弧长公式即可求出
所对圆心角的度数,再由AC的长求出半径,利用弧长公式即可求出![]() 的长,即可求出点F所经过的路径长.
的长,即可求出点F所经过的路径长.
连接AC,AO.
∵AB⊥CD,∴G为AB的中点,即AG=BG=![]() AB.
AB.
∵⊙O的半径为4,弦AB⊥CD且过半径OD的中点,∴OG=2,∴在Rt△AOG中,根据勾股定理得:AG=![]() =2
=2![]() ,∴AB=2AG=4
,∴AB=2AG=4![]() .
.
又∵CG=CO+GO=4+2=6,∴在Rt△AGC中,根据勾股定理得:AC=![]() =4
=4![]() .
.
∵CF⊥AE,∴△ACF始终是直角三角形,点F的运动轨迹为以AC为直径的半圆,当E位于点B时,CG⊥AE,此时F与G重合;当E位于D时,CA⊥AE,此时F与A重合,∴当点E从点B出发顺时针运动到点D时,点F所经过的路径长![]() .在Rt△ACG中,tan∠ACG=
.在Rt△ACG中,tan∠ACG=![]() =
=![]() ,∴∠ACG=30°,∴
,∴∠ACG=30°,∴![]() 所对圆心角的度数为60°.
所对圆心角的度数为60°.
∵直径AC=4![]() ,∴
,∴![]() 的长为
的长为![]() =
=![]() π,则当点E从点B出发顺时针运动到点D时,点F所经过的路径长为
π,则当点E从点B出发顺时针运动到点D时,点F所经过的路径长为![]() π.
π.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】维修一项工程,甲、乙两队合做,
 天能完成,共付工钱
天能完成,共付工钱 元,甲队每天的工钱比乙队多
元,甲队每天的工钱比乙队多 元.若两队独做,乙队工期是甲队的
元.若两队独做,乙队工期是甲队的 倍.
倍.(1)甲、乙两队独做各需多少天完成?
(2)若两队独做,哪队工钱总额较少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数
 图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(
图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),( ,y2)是抛物线上两点,则
,y2)是抛物线上两点,则y1>y2.其中说法正确的是( )
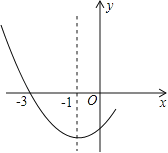
A. ①② B. ②③ C. ①②④ D. ②③④
-
科目: 来源: 题型:
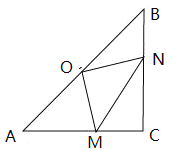
查看答案和解析>>【题目】如图,在
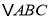 中,
中,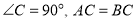 ,点
,点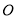 是
是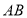 的中点.在
的中点.在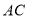 和
和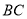 上.分别有一动点
上.分别有一动点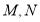 ,在移动过程中保持
,在移动过程中保持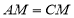 .
. 
(1)判断
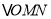 的形状,并说明理出.
的形状,并说明理出.(2)当
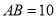 时,求四边形
时,求四边形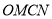 的面积.
的面积. -
科目: 来源: 题型:
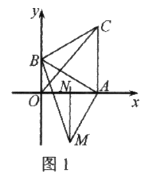
查看答案和解析>>【题目】如图1,直角坐标系中,点
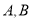 分别在
分别在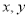 轴上,点
轴上,点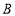 的坐标为
的坐标为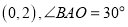 .以
.以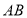 为边在第一象限作等边
为边在第一象限作等边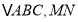 垂直平分
垂直平分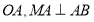 .
.
(1)求
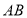 的长.
的长.(2)求证:
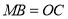 .
.(3)如图2,连接
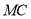 交
交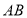 于点
于点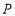 .点
.点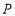 是否为MC的中点?请说明理由.
是否为MC的中点?请说明理由.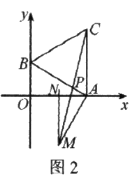
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线的解析式;
(2)当点P运动到什么位置时,△PAB的面积有最大值?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“如果二次函数
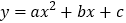 的图象与
的图象与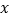 轴有两个公共点,那么一元二次方程
轴有两个公共点,那么一元二次方程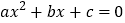 有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若
有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若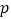 、
、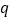 (
(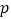 <
<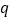 )是关于
)是关于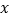 的方程
的方程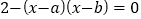 的两根且
的两根且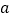 <
<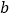 则请用“<”来表示
则请用“<”来表示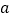 、
、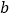 、
、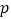 、
、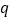 的大小是_________.
的大小是_________.
相关试题

