【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点.在
的中点.在![]() 和
和![]() 上.分别有一动点
上.分别有一动点![]() ,在移动过程中保持
,在移动过程中保持![]() .
.
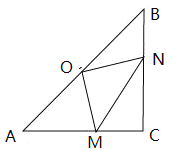
(1)判断![]() 的形状,并说明理出.
的形状,并说明理出.
(2)当![]() 时,求四边形
时,求四边形![]() 的面积.
的面积.
参考答案:
【答案】(1)等腰直角三角形,见解析;(2)![]()
【解析】
连接OC.先证得△OAM≌△CNO,然后根据全等三角形的对应边相等推知OM=ON;然后由等腰直角三角形ABC的性质、等腰三角形OMN的性质推知∠NOM=90°,即△OMN是等腰直角三角形;
(2)由(1)得△OAM≌△CNO,所以四边形![]() 的面积等于△OAC的面积,根据题意可得OC=OA =
的面积等于△OAC的面积,根据题意可得OC=OA =![]() AB=5,从而求解.
AB=5,从而求解.
解: (1)![]() 是等腰直角三角形.理由如下:
是等腰直角三角形.理由如下:
连接![]() .
.
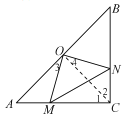
![]() ,点
,点![]() 是
是![]() 的中点,
的中点,
![]() (三线合一)
(三线合一)
![]() .
.
![]() .
.
![]()
![]() .
.
![]() ,
,
![]() .
.
![]() .
.
![]() .
.
![]() 是等腰直角三角形.
是等腰直角三角形.
(2)∵AB=10,∴OC=![]() AB=5=OA,
AB=5=OA,
由(1),![]() ,OC⊥AAB,
,OC⊥AAB,
![]() .
.
![]() .
.
-
科目: 来源: 题型:
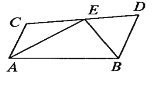
查看答案和解析>>【题目】如图,
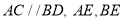 分别平分
分别平分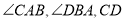 经过点
经过点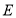 ,则
,则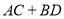 ( )
( )
A.
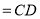 B.
B.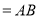 C.
C.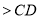 D.
D.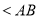
-
科目: 来源: 题型:
查看答案和解析>>【题目】维修一项工程,甲、乙两队合做,
 天能完成,共付工钱
天能完成,共付工钱 元,甲队每天的工钱比乙队多
元,甲队每天的工钱比乙队多 元.若两队独做,乙队工期是甲队的
元.若两队独做,乙队工期是甲队的 倍.
倍.(1)甲、乙两队独做各需多少天完成?
(2)若两队独做,哪队工钱总额较少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数
 图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(
图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),( ,y2)是抛物线上两点,则
,y2)是抛物线上两点,则y1>y2.其中说法正确的是( )
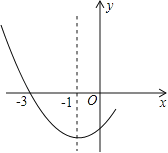
A. ①② B. ②③ C. ①②④ D. ②③④
-
科目: 来源: 题型:
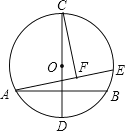
查看答案和解析>>【题目】如图,在半径为4的⊙O中,CD为直径,AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )
A.
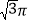 B.
B. 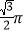 C.
C. 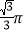 D.
D. 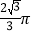
-
科目: 来源: 题型:
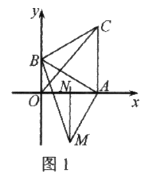
查看答案和解析>>【题目】如图1,直角坐标系中,点
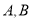 分别在
分别在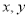 轴上,点
轴上,点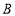 的坐标为
的坐标为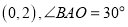 .以
.以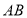 为边在第一象限作等边
为边在第一象限作等边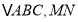 垂直平分
垂直平分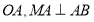 .
.
(1)求
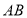 的长.
的长.(2)求证:
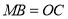 .
.(3)如图2,连接
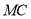 交
交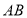 于点
于点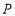 .点
.点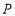 是否为MC的中点?请说明理由.
是否为MC的中点?请说明理由.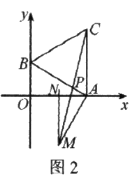
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线的解析式;
(2)当点P运动到什么位置时,△PAB的面积有最大值?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.

相关试题

