【题目】“如果二次函数![]() 的图象与
的图象与![]() 轴有两个公共点,那么一元二次方程
轴有两个公共点,那么一元二次方程![]() 有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若
有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若![]() 、
、![]() (
(![]() <
<![]() )是关于
)是关于![]() 的方程
的方程![]() 的两根且
的两根且![]() <
<![]() 则请用“<”来表示
则请用“<”来表示![]() 、
、![]() 、
、![]() 、
、![]() 的大小是_________.
的大小是_________.
参考答案:
【答案】p<a<b<q.
【解析】
依题意画出函数y=(x﹣a)(x﹣b)图象草图,根据二次函数的增减性求解.
依题意,画出函数y=(x﹣a)(x﹣b)的图象,如图所示.
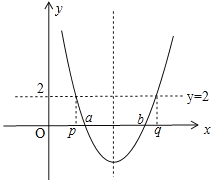
函数图象为抛物线,开口向上,与x轴两个交点的横坐标分别为a,b(a<b).
方程2﹣(x﹣a)(x﹣b)=0
转化为(x﹣a)(x﹣b)=2,方程的两根是抛物线y=(x﹣a)(x﹣b)与直线y=2的两个交点.
由p<q,可知对称轴左侧交点横坐标为p,右侧为q.
由抛物线开口向上,则在对称轴左侧,y随x增大而减少,则有p<a;在对称轴右侧,y随x增大而增大,则有b<q.
综上所述:可知p<a<b<q.
故答案为:p<a<b<q.
-
科目: 来源: 题型:
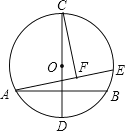
查看答案和解析>>【题目】如图,在半径为4的⊙O中,CD为直径,AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )
A.
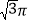 B.
B. 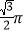 C.
C. 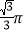 D.
D. 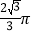
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直角坐标系中,点
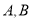 分别在
分别在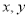 轴上,点
轴上,点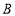 的坐标为
的坐标为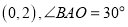 .以
.以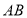 为边在第一象限作等边
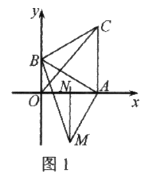
为边在第一象限作等边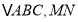 垂直平分
垂直平分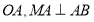 .
.
(1)求
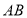 的长.
的长.(2)求证:
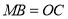 .
.(3)如图2,连接
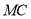 交
交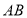 于点
于点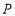 .点
.点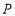 是否为MC的中点?请说明理由.
是否为MC的中点?请说明理由.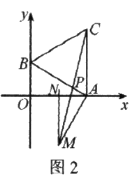
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线的解析式;
(2)当点P运动到什么位置时,△PAB的面积有最大值?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC与BD相交于点O,∠D=∠C,添加下列哪个条件后,仍不能使△ADO≌△BCO的是( )

A. AD=BC B. AC=BD C. OD=OC D. ∠ABD=∠BAC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE,下列说法:①△ABD 和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;⑤CE=AE.其中正确的是( )
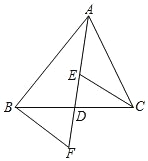
A. ①② B. ③⑤ C. ①③④ D. ①④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣2(m+1)x+m2+2=0.
(1)若方程总有两个实数根,求m的取值范围;
(2)若方程有一个实数根为1,求m的值和另一个根.
相关试题

