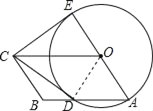
【题目】如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
(1)求证:CD是⊙O的切线;
(2)若BC=4,CD=6,求平行四边形OABC的面积.

参考答案:
【答案】(1)证明见解析(2)24
【解析】试题分析:(1)连接OD,求出∠EOC=∠DOC,根据SAS推出△EOC≌△DOC,推出∠ODC=∠OEC=90°,根据切线的判定推出即可;
(2)根据切线长定理求出CE=CD=4,根据平行四边形性质求出OA=OD=4,根据平行四边形的面积公式=2△COD的面积即可求解.
试题解析:(1)证明:连接OD,
∵OD=OA,
∴∠ODA=∠A,
∵四边形OABC是平行四边形,
∴OC∥AB,
∴∠EOC=∠A,∠COD=∠ODA,
∴∠EOC=∠DOC,
在△EOC和△DOC中,
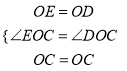
∴△EOC≌△DOC(SAS),
∴∠ODC=∠OEC=90°,
即OD⊥DC,
∴CD是⊙O的切线;
(2)由(1)知CD是圆O的切线,
∴△CDO为直角三角形,
∵S△CDO=![]() CDOD,
CDOD,
又∵OA=BC=OD=4,
∴S△CDO=![]() ×6×4=12,
×6×4=12,
∴平行四边形OABC的面积S=2S△CDO=24.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在第1个△ABA1中,∠B=40°,∠BAA1=∠BA1A,在A1B上取一点C,延长AA1到A2,使得在第2个△A1CA2中,∠A1CA2=∠A1 A2C;在A2C上取一点D,延长A1A2到A3,使得在第3个△A2DA3中,∠A2DA3=∠A2 A3D;…,按此做法进行下去,第3个三角形中以A3为顶点的内角的度数为 ;第n个三角形中以An为顶点的内角的度数为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 与
与 关于直线
关于直线 对称,
对称, ,延长
,延长 交
交 于点
于点 ,当
,当 ______时,
______时, 是等腰三角形.
是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近日,深圳市人民政府发布了《深圳市可持续发展规划》,提出了要做可持续发展的全球创新城市的目标,某初中学校了解学生的创新意识,组织了全校学生参加创新能力大赛,从中抽取了部分学生成绩,分为5组:A组50~60;B组60~70;C组70~80;D组80~90;E组90~100,统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.
(1)抽取学生的总人数是 人,扇形C的圆心角是 °;
(2)补全频数直方图;
(3)该校共有2200名学生,若成绩在70分以下(不含70分)的学生创新意识不强,有待进一步培养,则该校创新意识不强的学生约有多少人?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数学活动课上,小丽为了测量校园内旗杆AB的高度,站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.已知旗杆与教学楼的距离BD=9m,请你帮她求出旗杆的高度(结果保留根号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】问题:探究函数y=|x|﹣2的图象与性质.
小华根据学习函数的经验,对函数y=|x|﹣2的图象与性质进行了探究.
下面是小华的探究过程,请补充完整:
(1)在函数y=|x|﹣2中,自变量x可以是任意实数;
(2)如表是y与x的几组对应值.
x
…
﹣3
﹣2
﹣1
0
1
2
3
…
y
…
1
0
﹣1
﹣2
﹣1
0
m
…
①m= ;
②若A(n,8),B(10,8)为该函数图象上不同的两点,则n= ;
(3)如图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点.并根据描出的点,画出该函数的图象;
根据函数图象可得:
①该函数的最小值为 ;
②已知直线
 与函数y=|x|﹣2的图象交于C、D两点,当y1≥y时x的取值范围是 .
与函数y=|x|﹣2的图象交于C、D两点,当y1≥y时x的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,
, ,
, 的面积为30,
的面积为30,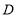 为
为 边上一动点(不与
边上一动点(不与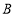 ,
, 重合),将
重合),将 和
和 分别沿直线
分别沿直线 ,
, 翻折得到
翻折得到 与
与 ,那么
,那么 的面积最小值为______.
的面积最小值为______.
相关试题

