【题目】问题:探究函数y=|x|﹣2的图象与性质.
小华根据学习函数的经验,对函数y=|x|﹣2的图象与性质进行了探究.
下面是小华的探究过程,请补充完整:
(1)在函数y=|x|﹣2中,自变量x可以是任意实数;
(2)如表是y与x的几组对应值.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 1 | 0 | ﹣1 | ﹣2 | ﹣1 | 0 | m | … |
①m= ;
②若A(n,8),B(10,8)为该函数图象上不同的两点,则n= ;
(3)如图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点.并根据描出的点,画出该函数的图象;
根据函数图象可得:
①该函数的最小值为 ;
②已知直线![]() 与函数y=|x|﹣2的图象交于C、D两点,当y1≥y时x的取值范围是 .
与函数y=|x|﹣2的图象交于C、D两点,当y1≥y时x的取值范围是 .

参考答案:
【答案】(1)补图见解析;(2)①1;②﹣10;(3)①﹣2;②﹣1≤x≤3.
【解析】
(2)①把x=3代入y=|x|-2,即可求出m;
②把y=8代入y=|x|-2,即可求出n;
(3)①画出该函数的图象即可求解;
②在同一平面直角坐标系中画出函数y1=![]() x
x![]() 与函数y=|x|-2的图象,根据图象即可求出y1≥y时x的取值范围.
与函数y=|x|-2的图象,根据图象即可求出y1≥y时x的取值范围.
解:(2)①把x=3代入y=|x|﹣2,得m=3﹣2=1.
故答案为1;
②把y=8代入y=|x|﹣2,得8=|x|﹣2,
解得x=﹣10或10,
∵A(n,8),B(10,8)为该函数图象上不同的两点,
∴n=﹣10.
故答案为﹣10;
(3)该函数的图象如图,
①该函数的最小值为﹣2;
故答案为﹣2;
②在同一平面直角坐标系中画出函数y1=![]() x-
x-![]() 与函数y=|x|﹣2的图象,
与函数y=|x|﹣2的图象,
由图形可知,当y1≥y时x的取值范围是﹣1≤x≤3.
故答案为﹣1≤x≤3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近日,深圳市人民政府发布了《深圳市可持续发展规划》,提出了要做可持续发展的全球创新城市的目标,某初中学校了解学生的创新意识,组织了全校学生参加创新能力大赛,从中抽取了部分学生成绩,分为5组:A组50~60;B组60~70;C组70~80;D组80~90;E组90~100,统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.
(1)抽取学生的总人数是 人,扇形C的圆心角是 °;
(2)补全频数直方图;
(3)该校共有2200名学生,若成绩在70分以下(不含70分)的学生创新意识不强,有待进一步培养,则该校创新意识不强的学生约有多少人?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
(1)求证:CD是⊙O的切线;
(2)若BC=4,CD=6,求平行四边形OABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数学活动课上,小丽为了测量校园内旗杆AB的高度,站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.已知旗杆与教学楼的距离BD=9m,请你帮她求出旗杆的高度(结果保留根号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,
,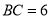 ,
, 的面积为30,
的面积为30,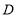 为
为 边上一动点(不与
边上一动点(不与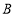 ,
, 重合),将
重合),将 和
和 分别沿直线
分别沿直线 ,
, 翻折得到
翻折得到 与
与 ,那么
,那么 的面积最小值为______.
的面积最小值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,先描出点
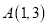 ,点
,点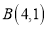 .
.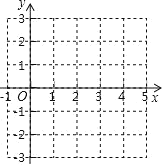
(1)描出点
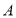 关于
关于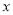 轴的对称点
轴的对称点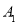 的位置,写出
的位置,写出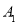 的坐标 ;
的坐标 ;(2)用尺规在
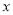 轴上找一点
轴上找一点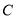 ,使
,使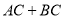 的值最小(保留作图痕迹);
的值最小(保留作图痕迹);(3)用尺规在
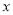 轴上找一点
轴上找一点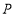 ,使
,使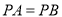 (保留作图痕迹).
(保留作图痕迹). -
科目: 来源: 题型:
查看答案和解析>>【题目】2013年某企业按餐厨垃圾处理费25元/吨,建筑垃圾处理费16元/吨标准,共支付餐厨和建筑垃圾处理费5200元,从2014年元月起,收费标准上调为:餐厨垃圾处理费100元/吨,建筑垃圾处理费30元/吨,若该企业2014年处理的这两种垃圾数量与2013年相比没有变化,就要多支付垃圾处理费8800元,
(1)该企业2013年处理的餐厨垃圾和建筑垃圾各多少吨?
(2)该企业计划2014年将上述两种垃圾处理量减少到240吨,且建筑垃圾处理费不超过餐厨垃圾处理量的3倍,则2014年该企业最少需要支付这两种垃圾处理费共多少元?
相关试题

