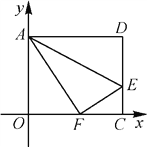
【题目】如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处,若点D的坐标为(10,8),求点E的坐标
参考答案:
【答案】(10,3)
【解析】根据折叠的性质得到AF=AD,所以在直角△AOF中,利用勾股定理来求OF=6,即可求出CF=10-6=4,然后设EC=x,则EF=DE=8-x,根据勾股定理列方程求出EC可得点E的坐标.
解:∵点D的坐标为(10,8),
∴AD=OC=10,AO=DC=8.
由翻折的性质可知:AF=AD=10,ED=EF.
在Rt△AOF中,由勾股定理得:
OF=![]() =6.
=6.
∴CF=OC-OF=4,
设EC=x,则EF = DE=8-x.
在Rt△EFC中,由勾股定理得:
x2+42=(8-x)2,
解得,x=3,
∴CE=3,
∴E(10,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,求这块空地的面积?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠B=∠C,AD∥BC.
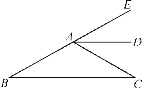
(1)证明:AD平分∠CAE;
(2)如果∠BAC=120°,求∠B的度数.(不允许使用三角形内角和为180°)
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读题:课本上有这样一道例题:“解方程:
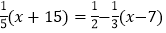
解:去分母得:
6(x+15)=15-10(x-7)①
6x+90=15-10x+70②
16x=-5③
x=-
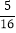 ④
④请回答下列问题:
(1)得到①式的依据是________;
(2)得到②式的依据是________;
(3)得到③式的依据是________;
(4)得到④式的依据是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大学生小刘回乡创办小微企业,初期购得原材料若干吨,每天生产相同件数的某种产品,单件产品所耗费的原材料相同.当生产6天后剩余原材料36吨,当生产10天后剩余原材料30吨.若剩余原材料数量小于或等于3吨,则需补充原材料以保证正常生产.
(1)求初期购得的原材料吨数与每天所耗费的原材料吨数;
(2)若生产16天后,根据市场需求每天产量提高20%,则最多再生产多少天后必须补充原材料?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:(1)2∠DCF=∠BCD,(2)EF=CF;(3)S△BEC=2S△CEF;(4)∠DFE=3∠AEF.
其中正确结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)2(x-2)-3(4x-1)=9(1-x); (2)
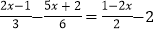 ;
;(3)
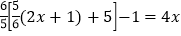 ; (4)
; (4)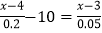 ;
;(5)
 .
.
相关试题

