【题目】如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,求这块空地的面积?

参考答案:
【答案】这块空地的面积是24平方米.
【解析】连接AC,先利用勾股定理求出AC,再利用勾股定理的逆定理证出△ABC是直角三角形,最后将Rt△ABC与Rt△ACD的面积作差即可得出答案.
解:连接AC,

在Rt△ACD中,
∵∠ADC=90°,AD=4米,CD=3米,
∴由勾股定理得:AC=5(米),
∵AC2+BC2=52+122=169,AB2=132=169,
∴AC2+BC2=AB2,
∴∠ACB=90°,
该区域面积S=S△ACB-S△ADC=![]() ×5×12-
×5×12-![]() ×3×4=24(平方米)
×3×4=24(平方米)
答:这块空地的面积是24平方米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中错误的是( )

A.b2>4ac
B.ax2+bx+c≥﹣6
C.若点(﹣2,m),(﹣5,n)在抛物线上,则m>n
D.关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,点P是CD的中点,∠BCD=60°,射线AP交BC的延长线于点E,射线BP交DE于点K,点O是线段BK的中点,作BM⊥AE于点M,作KN⊥AE于点N,连结MO、NO,以下四个结论:①△OMN是等腰三角形;②tan∠OMN=
 ;③BP=4PK;④PMPA=3PD2 , 其中正确的是( )
;③BP=4PK;④PMPA=3PD2 , 其中正确的是( )
A.①②③
B.①②④
C.①③④
D.②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】根据等式和不等式的性质,可以得到:若a﹣b>0,则a>b;若a﹣b=0,则a=b;若a﹣b<0,则a<b.这是利用“作差法”比较两个数或两个代数式值的大小.
(1)试比较代数式5m2﹣4m+2与4m2﹣4m﹣7的值之间的大小关系;
(2)已知A=5m2﹣4(
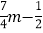 ),B=7(m2﹣m)+3,请你运用前面介绍的方法比较代数式A与B的大小.
),B=7(m2﹣m)+3,请你运用前面介绍的方法比较代数式A与B的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠B=∠C,AD∥BC.
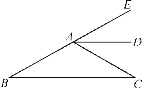
(1)证明:AD平分∠CAE;
(2)如果∠BAC=120°,求∠B的度数.(不允许使用三角形内角和为180°)
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读题:课本上有这样一道例题:“解方程:
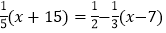
解:去分母得:
6(x+15)=15-10(x-7)①
6x+90=15-10x+70②
16x=-5③
x=-
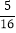 ④
④请回答下列问题:
(1)得到①式的依据是________;
(2)得到②式的依据是________;
(3)得到③式的依据是________;
(4)得到④式的依据是________.
-
科目: 来源: 题型:
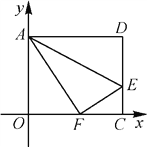
查看答案和解析>>【题目】如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处,若点D的坐标为(10,8),求点E的坐标
相关试题

