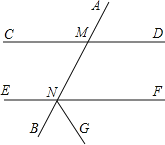
【题目】如图,已知NG平分∠BNF,∠AMD=∠MNF,∠CMN:∠DMN=3:5,试求∠MNF和∠GNF的度数.
参考答案:
【答案】∠MNF=67.5°,∠GNF=56.25°
【解析】
先利用平角的定义得到∠CMN=67.5°,∠CMN=112.5°,再根据平行线的判定由∠AMD=∠MNF得到CD∥EF,于是根据平行线的性质得∠MNF=∠CMN=67.5°,∠BNF=∠DMN=112.5°,然后根据角平分线的定义求∠GNF的度数.
解:∵∠CMN:∠DMN=3:5,
而∠CMN+∠DMN=180°,
∴∠CMN=![]() ×180°=67.5°,∠CMN=
×180°=67.5°,∠CMN=![]() ×180°=112.5°,
×180°=112.5°,
∵∠AMD=∠MNF,
∴CD∥EF,
∴∠MNF=∠CMN=67.5°,
∠BNF=∠DMN=112.5°,
∵NG平分∠BNF,
∴∠GNF=![]() ∠BNF=56.25°.
∠BNF=56.25°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D.下列四个命题:①当x>0时,y>0; ②若a=﹣1,则b=3;③抛物线上有两点P(x1 , y1)和Q(x2 , y2),若x1<1<x2 , 且x1+x2>2,则y1>y2;④点C关于抛物线对称轴的对称点为E,点G,F分别在x轴和y轴上,当m=2时,四边形EDFG周长的最小值为6
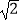 .其中正确的命题有( )个.
.其中正确的命题有( )个.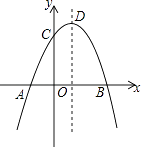
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,当运动时间为s时,四边形EFGH的面积最小,其最小值是cm2 .
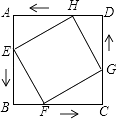
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+2过点A(﹣2,0),B(2,2),与y轴交于点C.

(1)求抛物线y=ax2+bx+2的函数表达式;
(2)若点D在抛物线y=ax2+bx+2的对称轴上,求△ACD的周长的最小值;
(3)在抛物线y=ax2+bx+2的对称轴上是否存在点P,使△ACP是直角三角形?若存在直接写出点P的坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD.
(1)求证:AB=AD;
(2)求证:CD平分∠ACE.
(3)猜想∠BDC与∠BAC之间有何数量关系?并对你的猜想加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】判断下列式子中,哪些是一元一次不等式组?
(1)
 ;(2)
;(2) ;(3)
;(3) ;(4)
;(4) ;(5)
;(5) .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了对学生进行爱国主义教育,某校组织学生去看演出,有甲乙两种票,已知甲乙两种票的单价比为4:3,单价和为42元.
(1)甲乙两种票的单价分别是多少元?
(2)学校计划拿出不超过750元的资金,让七年级一班的36名学生首先观看,且规定购买甲种票必须多于15张,有哪几种购买方案?
相关试题

