搜索
【题目】如图，在边长为6cm的正方形ABCD中，点E、F、G、H分别从点A、B、C、D同时出发，均以1cm/s的速度向点B、C、D、A匀速运动，当点E到达点B时，四个点同时停止运动，在运动过程中，当运动时间为s时，四边形EFGH的面积最小，其最小值是cm2 ．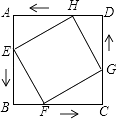 
参考答案：
【答案】3；18
【解析】解：设运动时间为t（0≤t≤6），则AE=t，AH=6﹣t， 根据题意得：S四边形EFGH=S正方形ABCD﹣4S△AEH=6×6﹣4× 
t（6﹣t）=2t2﹣12t+36=2（t﹣3）2+18，
∴当t=3时，四边形EFGH的面积取最小值，最小值为18．
所以答案是：3；18
【考点精析】本题主要考查了二次函数的最值和正方形的性质的相关知识点，需要掌握如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a；正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】对于实数p，q，我们用符号min{p，q}表示p，q两数中较小的数，如min{1，2}=1，因此，min{﹣
，﹣ 
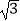}=；若min{（x﹣1）2 ， x2}=1，则x= ． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知下列关于
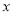的分式方程:方程1.
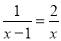, 方程2. 
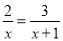, 方程3. 
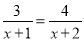, ……,方程n,【1】填空：分式方程1的解为 ，分式方程2的解为 ；
【2】解分式方程3；
【3】根据上述方程的规律及解的特点，直接写出方程n及它的解.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=﹣x2+2x+m+1交x轴于点A（a，0）和B（b，0），交y轴于点C，抛物线的顶点为D．下列四个命题：①当x＞0时，y＞0； ②若a=﹣1，则b=3；③抛物线上有两点P（x1 ， y1）和Q（x2 ， y2），若x1＜1＜x2 ， 且x1+x2＞2，则y1＞y2；④点C关于抛物线对称轴的对称点为E，点G，F分别在x轴和y轴上，当m=2时，四边形EDFG周长的最小值为6
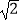．其中正确的命题有（ ）个．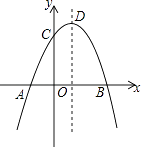
A.1
B.2
C.3
D.4 -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，抛物线y=ax2+bx+2过点A（﹣2，0），B（2，2），与y轴交于点C．
（1）求抛物线y=ax2+bx+2的函数表达式；
（2）若点D在抛物线y=ax2+bx+2的对称轴上，求△ACD的周长的最小值；
（3）在抛物线y=ax2+bx+2的对称轴上是否存在点P，使△ACP是直角三角形？若存在直接写出点P的坐标，若不存在，请说明理由． -
科目： 来源： 题型：
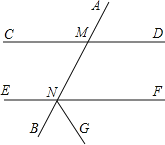
查看答案和解析>>【题目】如图，已知NG平分∠BNF，∠AMD=∠MNF，∠CMN：∠DMN=3：5，试求∠MNF和∠GNF的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知点A、C分别在∠GBE的边BG、BE上，且AB=AC，AD∥BE，∠GBE的平分线与AD交于点D，连接CD．
（1）求证：AB=AD；
（2）求证：CD平分∠ACE．
（3）猜想∠BDC与∠BAC之间有何数量关系？并对你的猜想加以证明．
相关试题
