【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+2过点A(﹣2,0),B(2,2),与y轴交于点C.
(1)求抛物线y=ax2+bx+2的函数表达式;
(2)若点D在抛物线y=ax2+bx+2的对称轴上,求△ACD的周长的最小值;
(3)在抛物线y=ax2+bx+2的对称轴上是否存在点P,使△ACP是直角三角形?若存在直接写出点P的坐标,若不存在,请说明理由.
参考答案:
【答案】
(1)
解:把点A(﹣2,0),B(2,2)代入抛物线y=ax2+bx+2中,
![]() ,
,
解得: 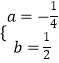 ,
,
∴抛物线函数表达式为:y=﹣ ![]() x2+
x2+ ![]() x+2
x+2
(2)
解:y=﹣ ![]() x2+
x2+ ![]() x+2=﹣
x+2=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() ;
;
∴对称轴是:直线x=1,
如图1,过B作BE⊥x轴于E,
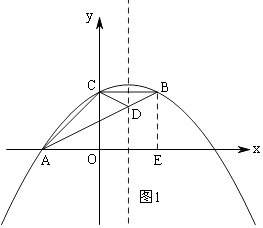
∵C(0,2),B(2,2),对称轴是:x=1,
∴C与B关于x=1对称,
∴CD=BD,
连接AB交对称轴于点D,此时△ACD的周长最小,
∵BE=2,AE=2+2=4,OC=2,OA=2,
∴AB= ![]() =2
=2 ![]() ,
,
AC= ![]() =2
=2 ![]() ,
,
∴△ACD的周长=AC+CD+AD=AC+BD+AD=AC+AB=2 ![]() +2
+2 ![]() ;
;
答:△ACD的周长的最小值是2 ![]() +2
+2 ![]()
(3)
解:存在,
分两种情况:
①当∠ACP=90°时,△ACP是直角三角形,如图2,
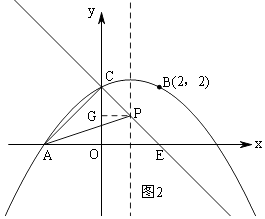
过P作PD⊥y轴于D,
设P(1,y),
则△CGP∽△AOC,
∴ ![]() ,
,
∴ ![]() ,
,
∴CG=1,
∴OG=2﹣1=1,
∴P(1,1);
②当∠CAP=90°时,△ACP是直角三角形,如图3,
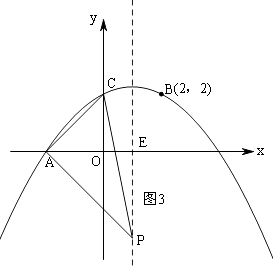
设P(1,y),
则△PEA∽△AOC,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴PE=3,
∴P(1,﹣3);
综上所述,△ACP是直角三角形时,点P的坐标为(1,1)或(1,﹣3).
【解析】(1)利用待定系数法求抛物线的函数表达式;(2)由轴对称的最短路径得:因为B与C关于对称轴对称,所以连接AB交对称轴于点D,此时△ACD的周长最小,利用勾股定理求其三边相加即可;(3)存在,当A和C分别为直角顶点时,画出直角三角形,设P(1,y),根据三角形相似列比例式可得P的坐标.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知下列关于
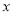 的分式方程:
的分式方程:方程1.
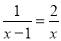 , 方程2.
, 方程2. 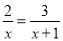 , 方程3.
, 方程3. 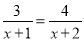 , ……,方程n,
, ……,方程n,【1】填空:分式方程1的解为 ,分式方程2的解为 ;
【2】解分式方程3;
【3】根据上述方程的规律及解的特点,直接写出方程n及它的解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D.下列四个命题:①当x>0时,y>0; ②若a=﹣1,则b=3;③抛物线上有两点P(x1 , y1)和Q(x2 , y2),若x1<1<x2 , 且x1+x2>2,则y1>y2;④点C关于抛物线对称轴的对称点为E,点G,F分别在x轴和y轴上,当m=2时,四边形EDFG周长的最小值为6
 .其中正确的命题有( )个.
.其中正确的命题有( )个.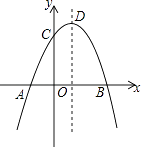
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,当运动时间为s时,四边形EFGH的面积最小,其最小值是cm2 .
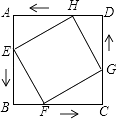
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知NG平分∠BNF,∠AMD=∠MNF,∠CMN:∠DMN=3:5,试求∠MNF和∠GNF的度数.
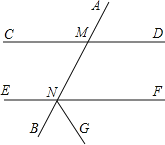
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD.
(1)求证:AB=AD;
(2)求证:CD平分∠ACE.
(3)猜想∠BDC与∠BAC之间有何数量关系?并对你的猜想加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】判断下列式子中,哪些是一元一次不等式组?
(1)
 ;(2)
;(2) ;(3)
;(3) ;(4)
;(4) ;(5)
;(5) .
.
相关试题

