【题目】如图,长方形ABCD中,AB=6cm,BC=4cm,点P从点A出发(不含点A),沿A→B→C→D运动,同时,点Q从点B出发(不含点B),沿B→C→D运动,当点P到达点B时,点Q恰好到达点C,已知点P每秒比点Q每秒多运动1cm,当其中一点到达点D(不含点D)时,另一点停止运动.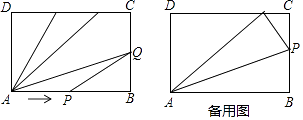
(1)求P、Q两点的速度;
(2)当其中一点到达点D时,另一点距离D点 cm(直接写答案);
(3)设点P、Q的运动时间为t(x),请用含t的代数式表示△APQ的面积为S(cm3),并写出t的取值范围.
参考答案:
【答案】
(1)
解:∵当点P到达点B时,点Q恰好到达点C,
∴P、Q两点的速度之比为:6:4=3:2,
设点P的速度是3xcm/s,则点Q的速度是2xcm/s,
由题意得,3x﹣2x=1,
解得,x=1,
∴点P的速度是3cm/s,则点Q的速度是2cm/s
(2)1
(3)
解:当0≤t≤2时,AP=3t,BQ=2t,
∴△APQ的面积为S= ![]() ×AP×BQ=3t2,
×AP×BQ=3t2,
当2<t≤ ![]() 时,BP=3t﹣6,CP=10﹣3t,CQ=2t﹣4,QD=10﹣2t,
时,BP=3t﹣6,CP=10﹣3t,CQ=2t﹣4,QD=10﹣2t,
∴△APQ的面积为S=6×4﹣ ![]() ×6×(3t﹣6)﹣
×6×(3t﹣6)﹣ ![]() ×4×(10﹣2t)﹣
×4×(10﹣2t)﹣ ![]() ×(10﹣3t)×(2t﹣4)=3t2﹣21t+42,
×(10﹣3t)×(2t﹣4)=3t2﹣21t+42,
当 ![]() <t≤5时,PQ=6﹣(3t﹣10)﹣[6﹣(2t﹣4)]=6﹣t,
<t≤5时,PQ=6﹣(3t﹣10)﹣[6﹣(2t﹣4)]=6﹣t,
∴△APQ的面积为S= ![]() ×PQ×AD=12﹣2t
×PQ×AD=12﹣2t
【解析】(2)点P到达点D所需的时间为:(6+4+6)÷3= ![]() s,
s,
点Q到达点D所需的时间为:(6+4)÷2=5s,
∴点Q先到达点D,
则点P距离D点16﹣3×5=1cm,
所以答案是:1;
【考点精析】关于本题考查的等腰直角三角形和翻折变换(折叠问题),需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣22+3×(﹣1)4﹣(﹣4)×2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OM⊥AB.
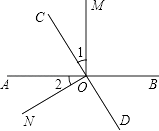
(1)若∠1=∠2,求∠NOD.
(2)若∠1= ∠BOC,求∠AOC与∠MOD.
∠BOC,求∠AOC与∠MOD. -
科目: 来源: 题型:
查看答案和解析>>【题目】规定一种新运算:a*b=a+b,ab=a﹣b,其中a、b为有理数,如a=2,b=1时,a*b=2+1=3,ab=2﹣1=1根据以上的运算法则化简:a2b*3ab+5a2b4ab,并求出当a=5,b=3时多项式的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料: 如图1,在Rt△ABC中,∠C=90°,D为边AC上一点,DA=DB,E为BD延长线上一点,∠AEB=120°,猜想AC、BE、AE的数量关系,并证明.
小明的思路是:根据等腰△ADB的轴对称性,将整个图形沿着AB边的垂直平分线翻折,得到点C的对称点F,如图2,过点A作AF⊥BE,交BE的延长线于F,请补充完成此问题;
参考小明思考问题的方法,解答下列问题:
如图3,等腰△ABC中,AB=AC,D、F在直线BC上,DE=BF,连接AD,过点E作EG∥AC交FH的延长线于点G,∠DFG+∠D=∠BAC.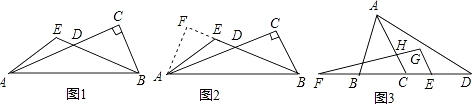
(1)探究∠BAD与∠CHG的数量关系;
(2)请在图中找出一条和线段AD相等的线段,并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知同一平面上的两个角的两条边分别平行,则这两个角( )
A. 相等 B. 互补 C. 相等或互补 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知Rt△ABC中,∠B=90°,AC=20,AB=10,P是边AC上一点(不包括端点A、C),过点P作PE⊥BC于点E,过点E作EF∥AC,交AB于点F.设PC=x,PE=y.
(1)求y与x的函数关系式;
(2)是否存在点P使△PEF是Rt△?若存在,求此时的x的值;若不存在,请说明理由.

相关试题

