【题目】在一条不完整的数轴上从左到右有点A,B,D,C,其中AB=2,BD=3,DC=1,如图所示,设点A,B,D,C所对应数的和是p.
![]()
(1)①若以B为原点.写出点A,D,C所对应的数,并计算p的值;
②若以D为原点,p的值是 若以C为原点,p的值是 .
(2)若原点O在图中数轴上点C的右边,且CO=15,p的值是 .
参考答案:
【答案】(1)①﹣2,3,4;5;②﹣7,﹣11;(2)-71
【解析】
(1)①根据已知点![]() 到点
到点![]() 的距离是
的距离是![]() 和点
和点![]() 到点
到点![]() 的距离分别是
的距离分别是![]() 即可求出点A,D,C所对应的数以及p的值;
即可求出点A,D,C所对应的数以及p的值;
②同理计算出以D为原点时点A,B,C所对应的数以及以C为原点时,点A,B,D所对应的数,即可求出p的值;
(2)原点O在图中数轴上点C的右边,且CO=15得到C的坐标为![]() ,易求得A、B、D的坐标,即可求得答案.
,易求得A、B、D的坐标,即可求得答案.
解:(1)①若以B为原点,
∵AB=2,BD=3,DC=1
∴点A,D,C所对应的数分别为:﹣2,3,4;
p=﹣2+3+4=5;
②若以D为原点,
∵AB=2,BD=3,DC=1
∴点A,B,C所对应的数分别为:﹣5,-3,1;
p=﹣5﹣3+1=﹣7;
若以C为原点,
∵AB=2,BD=3,DC=1
∴点A,B,D所对应的数分别为:﹣6,-4,-1;
p=﹣6﹣4﹣1=﹣11;
(2)若原点O在图中数轴上点C的右边,且CO=15,
∴点A,B,D,C所对应的数分别为:﹣21,-19,-16,-15,
则p=﹣21﹣19﹣16﹣15=﹣71.
故答案为:﹣71.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,点A(1,0),B(4,1),C(4,3),反比例函数y=
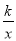 的图象经过点D,点P是一次函数y=mx+3﹣4m(m≠0)的图象与该反比例函数图象的一个公共点;
的图象经过点D,点P是一次函数y=mx+3﹣4m(m≠0)的图象与该反比例函数图象的一个公共点;(1)求反比例函数的解析式;
(2)通过计算说明一次函数y=mx+3﹣4m的图象一定过点C;
(3)对于一次函数y=mx+3﹣4m(m≠0),当y随x的增大而增大时,确定点P的横坐标的取值范围,(不必写过程)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B是线段AC上一点,AC=4AB,AB=6cm,直线MN经过线段BC的中点P.
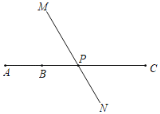
(1)图中共有线段_____条,图中共有射线_____条.
(2)图中与∠MPC互补的角是_____.
(3)线段AP的长度是_____.
-
科目: 来源: 题型:
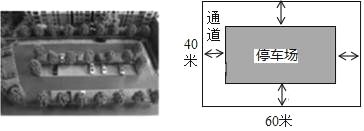
查看答案和解析>>【题目】如图,城市规划部门计划在城市广场的一块长方形空地上修建乙面积为1500m2的停车场,将停车场四周余下的空地修建成同样宽的通道,已知长方形空地的长为60m,宽为40m.
(1)求通道的宽度;
(2)某公司承揽了修建停车场的工程(不考虑修通道),为了尽量减少施工对城市交通的影响,实施施工时,每天的工作效率比原计划增加了20%,结果提前2天完成任务,求该公司原计划每天修建多少m2?
-
科目: 来源: 题型:
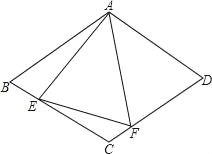
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,E、F在菱形的边BC,CD上.
(1)证明:BE=CF.
(2)当点E,F分别在边BC,CD上移动时(△AEF保持为正三角形),请探究四边形AECF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
(3)在(2)的情况下,请探究△CEF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标平面内,直线y=
 x+2分别与x轴、y轴交于点A、C.抛物线y=﹣
x+2分别与x轴、y轴交于点A、C.抛物线y=﹣ +bx+c经过点A与点C,且与x轴的另一个交点为点B.点D在该抛物线上,且位于直线AC的上方.
+bx+c经过点A与点C,且与x轴的另一个交点为点B.点D在该抛物线上,且位于直线AC的上方.(1)求上述抛物线的表达式;
(2)联结BC、BD,且BD交AC于点E,如果△ABE的面积与△ABC的面积之比为4:5,求∠DBA的余切值;
(3)过点D作DF⊥AC,垂足为点F,联结CD.若△CFD与△AOC相似,求点D的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOC与∠BOD具有公共顶点,∠COD是两个角叠合的部分.
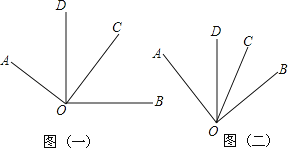
(1)若∠AOC=∠BOD=90°,观察图形(一)并完成下列问题:
①直接写出图中两个相等的锐角: = ;
②如果∠COD=40°,则∠AOB= ,若∠AOB=150°,则∠COD= ;
③猜想∠AOB+∠DOC= °,请说明理由.
(2)探究图形(二):若∠AOC=60°,∠BOD=50°,则∠AOB+∠DOC= °,请说明理由.
相关试题

