【题目】阅读下列材料,然后解答后面的问题.
我们知道方程2x+3y=12有无数组解,但在实际生活中我们往往只需要求出其正整数解.例:由2x+3y=12,得![]() ,(x、y为正整数)∴
,(x、y为正整数)∴![]() 则有0<x<6.又
则有0<x<6.又![]() 为正整数,则
为正整数,则![]() 为正整数.
为正整数.
由2与3互质,可知:x为3的倍数,从而x=3,代入![]() .
.
∴2x+3y=12的正整数解为![]()
问题:
(1)请你写出方程2x+y=5的一组正整数解:______;
(2)若![]() 为自然数,则满足条件的x值有______个;
为自然数,则满足条件的x值有______个;
A、2B、3C、4D、5
(3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
参考答案:
【答案】(1)当x=1时,y=3;当x=2时,y=1(2)C(3)有两种购买方案:即购买单价为3元的笔记本5本,单价为5元的钢笔4支;或购买单价为3元的笔记本10本,单价为5元的钢笔1支.
【解析】
根据题意可知,求方程的正整数解,先把方程做适当的变形,再列举正整数代入求解.(1)(2)参照例题的解题思路进行解答;
(3)设购买单价为3元的笔记本m本,单价为5元的钢笔n支.则根据题意得:3m+5n=35,其中m、n均为自然数.参照例题的解题思路解该二元一次方程即可.
解:(1)由2x+y=5,得y=5-2x(x、y为正整数).
所以![]() ,即0<x<
,即0<x<![]()
∴当x=1时,y=3;
当x=2时,y=1.
即方程的正整数解是![]() 或
或![]() ;
;
(2)同样,若![]() 为自然数,
为自然数,
则有:0<x-2≤6,即2<x≤8.
当x=3时,![]() ;
;
当x=4时,![]() ;
;
当x=5时,![]() ;
;
当x=8时,![]() .
.
即满足条件x的值有4个,
故选C;
(3)设购买单价为3元的笔记本m本,单价为5元的钢笔n支.
则根据题意得:3m+5n=35,其中m、n均为自然数.
于是有:![]() ,
,
解得: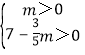 ,
,
所以0<m<![]() .
.
由于n=7-![]() m为正整数,则
m为正整数,则![]() m为正整数,可知m为5的倍数.
m为正整数,可知m为5的倍数.
∴当m=5时,n=4;
当m=10时,n=1.
答:有两种购买方案:即购买单价为3元的笔记本5本,单价为5元的钢笔4支;
或购买单价为3元的笔记本10本,单价为5元的钢笔1支.
故答案为:(1)当x=1时,y=3;当x=2时,y=1;(2)C;(3)有两种购买方案:即购买单价为3元的笔记本5本,单价为5元的钢笔4支;或购买单价为3元的笔记本10本,单价为5元的钢笔1支.
-
科目: 来源: 题型:
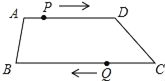
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:
AP= ;DP= ;BQ= ;CQ= .
(2)当t为何值时,四边形APQB是平行四边形?
(3)当t为何值时,四边形PDCQ是平行四边形?
-
科目: 来源: 题型:
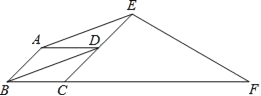
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠ABC=45°,E、F分别在CD和BC的延长线上,AE∥BD,∠EFC=30°, AB=2.
求CF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学七年级同学要在清明节到烈士陵园扫墓,计划制作
 朵小白花学生会主席小琳先做了
朵小白花学生会主席小琳先做了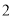 天,后来好朋友小雯也加入一起做了
天,后来好朋友小雯也加入一起做了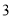 天,最后比计划多制作
天,最后比计划多制作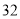 朵小白花.已知小雯每天比小琳少制作
朵小白花.已知小雯每天比小琳少制作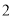 朵小白花.请问:小琳、小雯平均每天分别能制作多少朵小白花?
朵小白花.请问:小琳、小雯平均每天分别能制作多少朵小白花? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平行四边形ABCD中,E,F是对角线BD上的两点,且BF=DE.
求证:(1)AE=CF;
(2)四边形AECF是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN周长最小时,则∠AMN+∠ANM的度数是________

-
科目: 来源: 题型:
查看答案和解析>>【题目】学校“百变魔方”社团准备购买
 两种魔方.已知购买
两种魔方.已知购买 个
个 种魔方和
种魔方和 个
个 种魔方共需
种魔方共需 元;购买
元;购买 个
个 种魔方所需款数和购买
种魔方所需款数和购买 个
个 种魔方所需款数相同.优惠活动:活动一:“疯狂打折”:
种魔方所需款数相同.优惠活动:活动一:“疯狂打折”: 种魔方八折,
种魔方八折, 种魔方四折;活动二:“买一送一”:购买一个
种魔方四折;活动二:“买一送一”:购买一个 种魔方送一个
种魔方送一个 种魔方
种魔方(1)求
 这两种魔方的单价;
这两种魔方的单价;(2)结合社员们的需求,社团决定购买
 两种魔方共
两种魔方共 个(其中
个(其中 种魔方不超过
种魔方不超过 个) .某商店有两种优惠活动,如图所示.设购买
个) .某商店有两种优惠活动,如图所示.设购买 种魔方
种魔方 个,按活动一购买所需费用为
个,按活动一购买所需费用为 元,按活动二购买所需费用为
元,按活动二购买所需费用为 元.请根据以上信息,解决以下问题:
元.请根据以上信息,解决以下问题:
①试用含
 的代数式分别表示
的代数式分别表示 .
.②试求当购买
 种魔方多少个时,选择两种优惠活动同样实惠?
种魔方多少个时,选择两种优惠活动同样实惠?③以
 种魔方的个数说明选择哪种优惠活动购买魔方更实惠.
种魔方的个数说明选择哪种优惠活动购买魔方更实惠.
相关试题

