【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN周长最小时,则∠AMN+∠ANM的度数是________

参考答案:
【答案】120°
【解析】根据要使△AMN的周长最小,即利用点的对称,使三角形的三边在同一直线上,作出A关于BC和CD的对称点A′,A″,结合图形及已知条件,即可求出结果.
如图所示,当三角形三边在同一条直线上周长最短,作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN周长的最小值.作DA延长线AH,
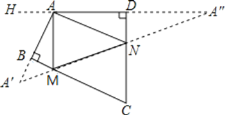
∵∠DAB=120°,
∴∠HAA′=60°,
∴∠AA′M+∠A″=∠HAA′=60°.
∵∠MA′A=∠MAA′,∠NAD=∠A″,且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×60°=120°.
故答案为:120°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学七年级同学要在清明节到烈士陵园扫墓,计划制作
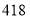 朵小白花学生会主席小琳先做了
朵小白花学生会主席小琳先做了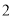 天,后来好朋友小雯也加入一起做了
天,后来好朋友小雯也加入一起做了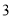 天,最后比计划多制作
天,最后比计划多制作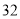 朵小白花.已知小雯每天比小琳少制作
朵小白花.已知小雯每天比小琳少制作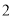 朵小白花.请问:小琳、小雯平均每天分别能制作多少朵小白花?
朵小白花.请问:小琳、小雯平均每天分别能制作多少朵小白花? -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,然后解答后面的问题.
我们知道方程2x+3y=12有无数组解,但在实际生活中我们往往只需要求出其正整数解.例:由2x+3y=12,得
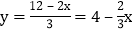 ,(x、y为正整数)∴
,(x、y为正整数)∴ 则有0<x<6.又
则有0<x<6.又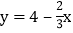 为正整数,则
为正整数,则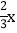 为正整数.
为正整数.由2与3互质,可知:x为3的倍数,从而x=3,代入
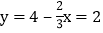 .
.∴2x+3y=12的正整数解为
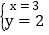
问题:
(1)请你写出方程2x+y=5的一组正整数解:______;
(2)若
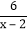 为自然数,则满足条件的x值有______个;
为自然数,则满足条件的x值有______个;A、2B、3C、4D、5
(3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平行四边形ABCD中,E,F是对角线BD上的两点,且BF=DE.
求证:(1)AE=CF;
(2)四边形AECF是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】学校“百变魔方”社团准备购买
 两种魔方.已知购买
两种魔方.已知购买 个
个 种魔方和
种魔方和 个
个 种魔方共需
种魔方共需 元;购买
元;购买 个
个 种魔方所需款数和购买
种魔方所需款数和购买 个
个 种魔方所需款数相同.优惠活动:活动一:“疯狂打折”:
种魔方所需款数相同.优惠活动:活动一:“疯狂打折”: 种魔方八折,
种魔方八折, 种魔方四折;活动二:“买一送一”:购买一个
种魔方四折;活动二:“买一送一”:购买一个 种魔方送一个
种魔方送一个 种魔方
种魔方(1)求
 这两种魔方的单价;
这两种魔方的单价;(2)结合社员们的需求,社团决定购买
 两种魔方共
两种魔方共 个(其中
个(其中 种魔方不超过
种魔方不超过 个) .某商店有两种优惠活动,如图所示.设购买
个) .某商店有两种优惠活动,如图所示.设购买 种魔方
种魔方 个,按活动一购买所需费用为
个,按活动一购买所需费用为 元,按活动二购买所需费用为
元,按活动二购买所需费用为 元.请根据以上信息,解决以下问题:
元.请根据以上信息,解决以下问题:
①试用含
 的代数式分别表示
的代数式分别表示 .
.②试求当购买
 种魔方多少个时,选择两种优惠活动同样实惠?
种魔方多少个时,选择两种优惠活动同样实惠?③以
 种魔方的个数说明选择哪种优惠活动购买魔方更实惠.
种魔方的个数说明选择哪种优惠活动购买魔方更实惠. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算: ﹣2﹣1+|
﹣2﹣1+|  ﹣2|﹣3sin30°
﹣2|﹣3sin30°
(2)先化简,再求值: ÷(
÷(  ﹣1),其中a=3.
﹣1),其中a=3. -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
 ,并求出所有正整数解的和.
,并求出所有正整数解的和.
相关试题

