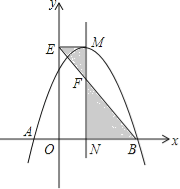
【题目】如图,抛物线![]() 与x轴交于A,B两点,它们的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F.已知点A的坐标为(﹣1,0).
与x轴交于A,B两点,它们的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F.已知点A的坐标为(﹣1,0).
(1)求该抛物线的解析式及顶点M的坐标;
(2)求△EMF与△BNF的面积之比.
参考答案:
【答案】(1)![]() ,(1,4);(2)
,(1,4);(2)![]() .
.
【解析】试题分析:(1)直接将(﹣1,0)代入求出即可,再利用配方法求出顶点坐标.
(2)利用EM∥BN,则△EMF∽△BNF,进而求出△EMF与△BNE的面积之比.
试题解析:解:(1)∵点A在抛物线![]() 上,
上,
∴![]() ,解得:c=3,
,解得:c=3,
∴抛物线的解析式为![]() .
.
∵![]() ,
,
∴抛物线的顶点M(1,4);
(2)∵A(﹣1,0),抛物线的对称轴为直线x=1,∴点B(3,0).
∴EM=1,BN=2.
∵EM∥BN,∴△EMF∽△BNF.∴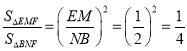 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的对角线AC,BD相交于点O,点E是AC的一点,连接EB,过点A做AM⊥BE,垂足为M,AM与BD相交于点F.
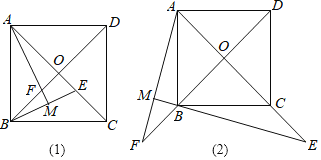
(1)猜想:如图(1)线段OE与线段OF的数量关系为 ;
(2)拓展:如图(2),若点E在AC的延长线上,AM⊥BE于点M,AM、DB的延长线相交于点F,其他条件不变,(1)的结论还成立吗?如果成立,请仅就图(2)给出证明;如果不成立,请说明理由.
-
科目: 来源: 题型:
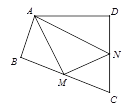
查看答案和解析>>【题目】四边形ABCD中,∠B=∠D=90°,∠C=72°,在BC、CD上分别找一点M、N,使△AMN的周长最小时,∠AMN+∠ANM的度数为_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点.
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;

(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】传统文化与我们生活息息相关,中华传统文化包括古文古诗、词语、乐曲、赋、民族音乐、民族戏剧、曲艺、国画、书法、对联、灯谜、射覆、酒令、歇后语等.在中华优秀传统文化进校园活动中,某校为学生请“戏曲进校园”和民族音乐”做节目演出,其中一场“戏曲进校园”的价格比一场“民族音乐”节目演出的价格贵600元,用20000元购买“戏曲进校园”的场数是用8800元购买“民族音乐节目演出场数的2倍,求一场“民族音乐”节目演出的价格.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 与
与 (
( )在同一直角坐标系中的大致图象可能是( )
)在同一直角坐标系中的大致图象可能是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O为原点,A. B为数轴上两点,AB=15,且OA:OB=2.
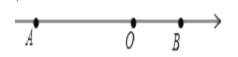
(1)A、B对应的数分别为___、___;
(2)点A. B分别以4个单位/秒和3个单位/秒的速度相向而行,则几秒后A. B相距1个单位长度?
(3)点A. B以(2)中的速度同时向右运动,点P从原点O以7个单位/秒的速度向右运动,是否存在常数m,使得4AP+3OBmOP为定值,若存在请求出m值以及这个定值;若不存在,请说明理由。
相关试题

