【题目】如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
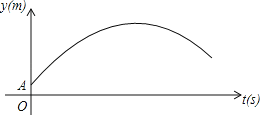
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?
参考答案:
【答案】(1)当t=![]() 时,y最大=4.5;(2)他能将球直接射入球门.
时,y最大=4.5;(2)他能将球直接射入球门.
【解析】
试题分析:(1)由题意得:函数y=at2+5t+c的图象经过(0,0.5)(0.8,3.5),于是得到![]() ,求得抛物线的解析式为:y=﹣
,求得抛物线的解析式为:y=﹣![]() t2+5t+
t2+5t+![]() ,当t=
,当t=![]() 时,y最大=4.5;
时,y最大=4.5;
(2)把x=28代入x=10t得t=2.8,当t=2.8时,y=﹣![]() ×2.82+5×2.8+
×2.82+5×2.8+![]() =2.25<2.44,于是得到他能将球直接射入球门.
=2.25<2.44,于是得到他能将球直接射入球门.
解:(1)由题意得:函数y=at2+5t+c的图象经过(0,0.5)(0.8,3.5),
∴![]() ,
,
解得: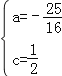 ,
,
∴抛物线的解析式为:y=﹣![]() t2+5t+
t2+5t+![]() ,
,
∴当t=![]() 时,y最大=4.5;
时,y最大=4.5;
(2)把x=28代入x=10t得t=2.8,
∴当t=2.8时,y=﹣![]() ×2.82+5×2.8+
×2.82+5×2.8+![]() =2.25<2.44,
=2.25<2.44,
∴他能将球直接射入球门.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的议程:3xn-1+(m-2)x2 = 5是一元一次方程,则m =_____n =__
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地为了鼓励居民节约用水,决定实行两级收费制,即每月用水量不超过12吨(含12吨)时,每吨按政府补贴优惠价收费;每月超过12吨,超过部分每吨按市场调节价收费,小黄家1月份用水24吨,交水费42元.2月份用水20吨,交水费32元.
(1)求每吨水的政府补贴优惠价和市场调节价分别是多少元;
(2)设每月用水量为x吨,应交水费为y元,写出y与x之间的函数关系式;
(3)小黄家3月份用水26吨,他家应交水费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一张桌子的售价是238元,比一张椅子的3倍少2元,设一张椅子的售价是x元,则可得方程__________________________;
-
科目: 来源: 题型:
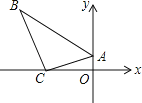
查看答案和解析>>【题目】一块直角三角板ABC按如图放置,顶点A的坐标为(0,1),直角顶点C的坐标为(﹣3,0),∠B=30°,则点B的坐标为( )
A.(﹣3﹣
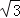 ,3)
,3) B.(﹣3﹣
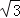 ,3
,3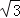 )
) C.(﹣
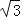 ,3)
,3) D.(﹣
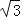 ,3
,3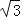 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,观察二次函数y=ax2+bx+c的图象,下列结论:
①a+b+c>0,②2a+b>0,③b2﹣4ac>0,④ac>0.
其中正确的是( )
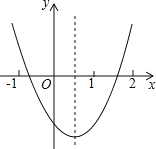
A.①② B.①④ C.②③ D.③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】—个多边形的内角和是外角和的4倍,则这个多边形是______边形.
相关试题

