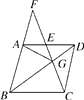
【题目】如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E,连接AG.
(1)求证:AG=CG;
(2)求证:AG2=GE·GF.

参考答案:
【答案】(1)证明见解析 (2)证明见解析
【解析】试题分析:
(1)由菱形的性质易证△ADG≌△CDG,从而可得AG=CG;
(2)由△ADG≌△CDG可得∠EAG=∠DCG,再由AB∥CD可得∠F=∠DCG,从而可得∠F=∠EAG,再利用∠AGE是公共角可证△AGE∽△FGA就可得到![]() ,所以
,所以![]()
试题解析:
(1)∵四边形ABCD是菱形,
∴AD=CD,∠ADB=∠CDB,
在△ADG与△CDG中, 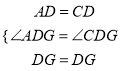 ,
,
∴△ADG≌△CDG,
∴AG=CG.
(2) ∵在菱形ABCD中,AB∥CD,
∴∠F=∠GCD.
∵△ADG≌△CDG,
∴∠EAG=∠DCG,
∴∠EAG=∠F.
又∵∠AGE=∠FGA,
∴△AGE∽△FGA,
∴![]() ,
,
∴AG2=GE·GF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=x2+bx+c的图象交x轴于A、B两点,交y轴于点C,顶点为点P,经过B、C两点的直线为y=﹣x+3.
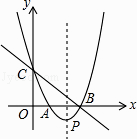
(1)求该二次函数的关系式;
(2)在该抛物线的对称轴上是否存在点M,使以点C、P、M为顶点的三角形是等腰三角形?若存在,请直接写出所有符合条件的点M的坐标;若不存在,请说明理由;
(3)连接AC,在x轴上是否存在点Q,使以点P、B、Q为顶点的三角形与△ABC相似?若存在,请求出点Q的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市水果批发部门欲将A市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为200元/时。其它主要参考数据如下:
运输工具
途中平均速度(千米/时)
运费(元/千米)
装卸费用(元)
火车
100
15
2000
汽车
80
20
900
(1)如果汽车的总支出费用比火车费用多1100元,你知道本市与A市之间的路程是多少千米吗?请你列方程解答.
(2)如果A市与某市之间的距离为S千米,且知道火车与汽车在路上耽误的时间分别为2小时和3.1小时,你若是某市水果批发部门的经理,要将这种水果从A市运往本市销售。你将选择哪种运输方式比较合算呢?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=kx2﹣6x+3,若k在数组(﹣3,﹣2,﹣1,1,2,3,4)中随机取一个,则所得抛物线的对称轴在直线x=1的右方时的概率为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=kx+b与函数y=
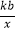 在同一坐标系中的大致图象正确的是( )
在同一坐标系中的大致图象正确的是( )
A.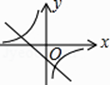
B.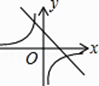
C.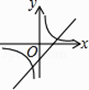
D.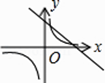
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形
 的边长
的边长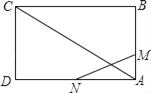 .某一时刻,动点
.某一时刻,动点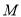 从
从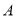 点出发沿
点出发沿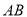 方向以
方向以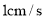 的速度向
的速度向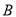 点匀速运动;同时,动点
点匀速运动;同时,动点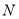 从
从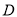 点出发沿
点出发沿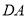 方向以
方向以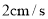 的速度向
的速度向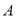 点匀速运动,问:
点匀速运动,问: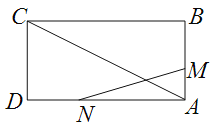
(1)经过多少时间,
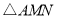 的面积等于矩形
的面积等于矩形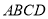 面积的
面积的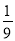 ?
?(2)是否存在时刻t,使以A,M,N为顶点的三角形与
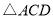 相似?若存在,求t的值;若不存在,请说明理由.
相似?若存在,求t的值;若不存在,请说明理由. -
科目: 来源: 题型:
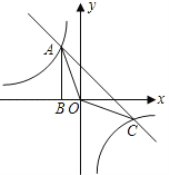
查看答案和解析>>【题目】如图,Rt△ABO的顶点A是双曲线y1=
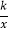 与直线y2=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y2=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO= .
.(1)求这两个函数的解析式;
(2)求△AOC的面积.
(3)直接写出使y1>y2成立的x的取值范围
相关试题

