【题目】如图,Rt△ABO的顶点A是双曲线y1=![]() 与直线y2=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y2=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=![]() .
.
(1)求这两个函数的解析式;
(2)求△AOC的面积.
(3)直接写出使y1>y2成立的x的取值范围
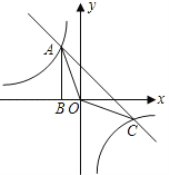
参考答案:
【答案】(1)y=﹣![]() ,y=﹣x+2;(2)4;(3)-1<x<0或x>3
,y=﹣x+2;(2)4;(3)-1<x<0或x>3
【解析】(1)欲求这两个函数的解析式,关键求k值.根据反比例函数性质,k绝对值为3且为负数,由此即可求出k;
(2)由函数的解析式组成方程组,解之求得A、C的坐标,然后根据S△AOC=S△ODA+S△ODC即可求出;
(3)根据图象即可求得.
解:(1)设A点坐标为(x,y),且x<0,y>0,
则S△ABO=![]() |BO||BA|=
|BO||BA|=![]() (﹣x)y=
(﹣x)y=![]() ,
,
∴xy=﹣3,
又∵y=![]() ,
,
即xy=k,
∴k=﹣3.
∴所求的两个函数的解析式分别为y=﹣![]() ,y=﹣x+2;
,y=﹣x+2;
(2)由y=﹣x+2,
令x=0,得y=2.
∴直线y=﹣x+2与y轴的交点D的坐标为(0,2),
∵A、C在反比例函数的图象上,
∴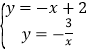 ,
,
解得![]() ,
,![]() ,
,
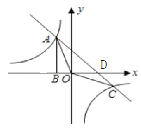
∴交点A(﹣1,3),C为(3,﹣1),
∴S△AOC=S△ODA+S△ODC=![]() OD(|x1|+|x2|)=
OD(|x1|+|x2|)=![]() ×2×(3+1)=4.
×2×(3+1)=4.
(3)-1<x<0或x>3 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E,连接AG.
(1)求证:AG=CG;
(2)求证:AG2=GE·GF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=kx+b与函数y=
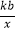 在同一坐标系中的大致图象正确的是( )
在同一坐标系中的大致图象正确的是( )
A.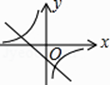
B.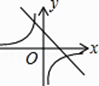
C.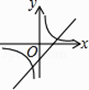
D.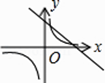
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形
 的边长
的边长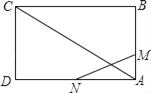 .某一时刻,动点
.某一时刻,动点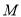 从
从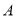 点出发沿
点出发沿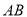 方向以
方向以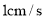 的速度向
的速度向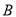 点匀速运动;同时,动点
点匀速运动;同时,动点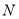 从
从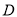 点出发沿
点出发沿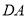 方向以
方向以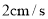 的速度向
的速度向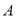 点匀速运动,问:
点匀速运动,问: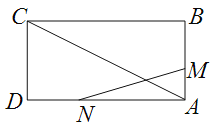
(1)经过多少时间,
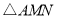 的面积等于矩形
的面积等于矩形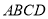 面积的
面积的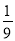 ?
?(2)是否存在时刻t,使以A,M,N为顶点的三角形与
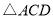 相似?若存在,求t的值;若不存在,请说明理由.
相似?若存在,求t的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了预防“甲型H1N1”,某校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量低于1.6mg时,生方可进教室,那么从消毒开始,至少需要几分钟后,生才能进入教室?
(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB、CD上),记它们的面积分别为SABCD和SBFDE . 现给出下列命题:
(i)若 =
= 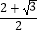 ,则tan∠EDF=
,则tan∠EDF= 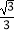
(ii)若DE2=BDEF,则DF=2AD
那么,下面判断正确的是( )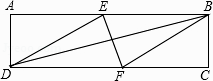
A.①正确,②正确
B.①正确,②错误
C.①错误,②正确
D.①错误,②错误 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数
 与方差s2如下表所示:
与方差s2如下表所示:甲
乙
丙
丁
平均数
 (cm)
(cm)561
560
561
560
方差s2
3.5
3.5
15.5
16.5
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A. 甲 B. 乙 C. 丙 D. 丁
相关试题

