【题目】如图,二次函数y=x2+bx+c的图象交x轴于A、B两点,交y轴于点C,顶点为点P,经过B、C两点的直线为y=﹣x+3.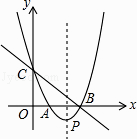
(1)求该二次函数的关系式;
(2)在该抛物线的对称轴上是否存在点M,使以点C、P、M为顶点的三角形是等腰三角形?若存在,请直接写出所有符合条件的点M的坐标;若不存在,请说明理由;
(3)连接AC,在x轴上是否存在点Q,使以点P、B、Q为顶点的三角形与△ABC相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:∵直线y=﹣x+3经过B、C两点,
∴B(3,0),C(0,3),
∵二次函数y=x2+bx+c图象交x轴于A、B两点,交y轴于点C,
∴ ![]() 解得
解得 ![]() ,
,
∴二次函数解析式为y=x2﹣4x+3
(2)
解:∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴该抛物线的对称轴为直线x=2,顶点坐标为P(2,﹣1),
∴如图1所示,满足条件的点M分别为
M1(2,7),M2(2,2 ![]() ﹣1),M3(2,
﹣1),M3(2, ![]() ),M4(2,﹣2
),M4(2,﹣2 ![]() ﹣1)
﹣1)

(3)
解:由(1)(2)得A(1,0),BP= ![]() ,BC=3
,BC=3 ![]() ,AB=2,
,AB=2,
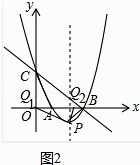
如图2所示,连接BP,∠CBA=∠ABP=45°,
① ![]() =
= ![]() 时,△ABC∽△PBQ1,
时,△ABC∽△PBQ1,
此时, ![]() =
= ![]() ,
,
∴BQ1=3,
∴Q1(0,0).
②当 ![]() =
= ![]() 时,△ABC∽△Q2BP,
时,△ABC∽△Q2BP,
此时, ![]() =
= ![]() ,
,
∴BQ2= ![]() ,
,
∴Q2( ![]() ,0),
,0),
综上所述,存在点Q使得以点P、B、Q为顶点的三角形与△ABC相似.
点Q坐标(0,0)或( ![]() ,0).
,0).
【解析】(1)先求出B、C坐标,代入抛物线解析式解方程组即可解决问题.(2)分三种情形讨论即可①CM=CP,②PM=PC,③MP=MC,画出图形即可解决问题.(3)分两种情形讨论即可① ![]() =
= ![]() 时,△ABC∽△PBQ1 , 列出方程即可解决.②当
时,△ABC∽△PBQ1 , 列出方程即可解决.②当 ![]() =
= ![]() 时,△ABC∽△Q2BP,列出方程即可解决.
时,△ABC∽△Q2BP,列出方程即可解决.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)-16+23+(-17)-(-7)
(2)
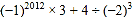
(3)
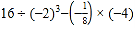
(4)(-8)÷(
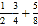 )-2×(-6)
)-2×(-6)(5)
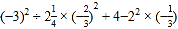
(6)(-
 )2×
)2× ÷|-
÷|-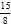 |+(-2)÷(
|+(-2)÷( )4
)4 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列变形中:
①由方程
 =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;②由方程
 x=
x= 两边同除以
两边同除以 ,得x=1;
,得x=1;③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣
 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1、x2.
(1)求实数k的取值范围.
(2)若方程两实根x1、x2满足x1+x2=﹣x1x2,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市水果批发部门欲将A市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为200元/时。其它主要参考数据如下:
运输工具
途中平均速度(千米/时)
运费(元/千米)
装卸费用(元)
火车
100
15
2000
汽车
80
20
900
(1)如果汽车的总支出费用比火车费用多1100元,你知道本市与A市之间的路程是多少千米吗?请你列方程解答.
(2)如果A市与某市之间的距离为S千米,且知道火车与汽车在路上耽误的时间分别为2小时和3.1小时,你若是某市水果批发部门的经理,要将这种水果从A市运往本市销售。你将选择哪种运输方式比较合算呢?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=kx2﹣6x+3,若k在数组(﹣3,﹣2,﹣1,1,2,3,4)中随机取一个,则所得抛物线的对称轴在直线x=1的右方时的概率为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E,连接AG.
(1)求证:AG=CG;
(2)求证:AG2=GE·GF.

相关试题

