【题目】边长为2的正方形ABCD与边长为2![]() 的正方形AEFG按图(1)位置放置,AD与AE在同一直线上,AB与AG在同一直线上,将正方形ABCD绕点A逆时针旋转如图(2),线段DG与线段BE相交,交点为H,则△GHE与△BHD面积之和的最大值为_________
的正方形AEFG按图(1)位置放置,AD与AE在同一直线上,AB与AG在同一直线上,将正方形ABCD绕点A逆时针旋转如图(2),线段DG与线段BE相交,交点为H,则△GHE与△BHD面积之和的最大值为_________ 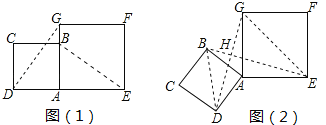
参考答案:
【答案】6
【解析】试题分析:)∵四边形ABCD和四边形AEFG都为正方形,
∴AD=AB,AG=AE,∠DAB=∠EAG=90°,
∴∠DAB+∠BAG =∠EAG+∠BAG,
∴∠DAG=∠BAE,
∴△ADG≌△ABE(SAS),
∴∠AGD=∠AEB,
在正方形AEFG中,∠AGE=∠AEG=45°,
∴∠HGE+∠HEG=45°+∠AGD+45°-∠AEB=90°,
所以∠GHE=90°,
所以对于△EGH,点H在以EG为直径的圆上,
∴当点H与点A重合时,△EGH的高最大;
同理对于△BDH,点H在以BD为直径的圆上,
∴当点H与点A重合时,△BDH的高最大,
∴△GHE和△BHD面积之和的最大值为: ![]() ×22+
×22+![]() ×(2
×(2![]() )2=2+4=6.
)2=2+4=6.
故答案为6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校准备从体育用品商店一次性购买若干个篮球和足球(每个篮球的价格相同,每个足球的价格相同),购买1个足球和2个篮球共需270元;购买2个足球和3个篮球共需440元.
(1)问足球和篮球的单价各是多少元?
(2)若购买足球和篮球共24个,且购买篮球的个数大于足球个数的2倍,购买球的总费用不超过2220元,问该学校有哪几种不同的购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°
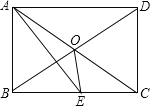
(1)求证:△ODC是等边三角形;
(2)求∠BOE
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线m∥AB,D为AB边上一点,过点D作DE⊥BC,交直线m于点E,垂足为点F,连接CD,BE.
(1)求证:CE=AD;
(2)当点D是AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)当∠A的大小满足什么条件时,四边形BECD是正方形?(不需要证明)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣(2m+1)x+m(m+1)=0,
(1)求证:方程总有两个不相等的实数根;
(2)设方程的两根分别为x1、x2,求
 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 在
在 的直径
的直径 的延长线上,点
的延长线上,点 在
在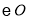 上,
上, 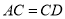 ,
,  ,
,
(1)求证:
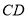 是
是 的切线;
的切线;(2)若
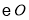 的半径为2,求图中阴影部分的面积.
的半径为2,求图中阴影部分的面积. -
科目: 来源: 题型:
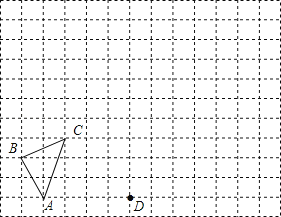
查看答案和解析>>【题目】如图,在由边长为1的单位正方形组成的网格中,按要求画出坐标系及△A1B1C1及△A2B2C2;
(1)若点A、C的坐标分别为(﹣3,0)、(﹣2,3),请画出平面直角坐标系并指出点B的坐标;
(2)画出△ABC关于y轴对称再向上平移1个单位后的图形△A1B1C1;
(3)以图中的点D为位似中心,将△A1B1C1作位似变换且把边长放大到原来的两倍,得到△A2B2C2.
相关试题

