搜索
【题目】如图，点
在
的直径
的延长线上，点
在
上， 
， 
，
（1）求证： 
是
的切线；
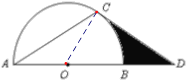
（2）若
的半径为2，求图中阴影部分的面积.
参考答案：
【答案】（1）证明见解析；（2）
.
【解析】试题分析：（1）连接OC．只需证明∠OCD＝90°．根据等腰三角形的性质即可证明；
（2）阴影部分的面积即为直角△OCD的面积减去扇形COB的面积．
试题解析：
（1）证明：连接OC，
∵AC＝CD，∠ACD＝120°，
∴∠CAD＝∠CDA＝30°，
∵OA＝OC，
∴∠CAD＝∠OCA＝30°，
∴∠COD＝60°
∴∠OCD＝90°，
∴CD是⊙O的切线；
（2）∵∠ACD＝30°，∠OCD＝90°，OC＝2，
在Rt△OCD中，
∵
＝tan60°，
∴CD＝2
，
S阴影＝S△COD－S扇形COB＝
.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ACB=90°，过点C的直线m∥AB，D为AB边上一点，过点D作DE⊥BC，交直线m于点E，垂足为点F，连接CD，BE．
（1）求证：CE=AD；
（2）当点D是AB中点时，四边形BECD是什么特殊四边形？说明你的理由；
（3）当∠A的大小满足什么条件时，四边形BECD是正方形？（不需要证明）
-
科目： 来源： 题型：
查看答案和解析>>【题目】边长为2的正方形ABCD与边长为2
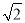的正方形AEFG按图（1）位置放置，AD与AE在同一直线上，AB与AG在同一直线上，将正方形ABCD绕点A逆时针旋转如图（2），线段DG与线段BE相交，交点为H，则△GHE与△BHD面积之和的最大值为_________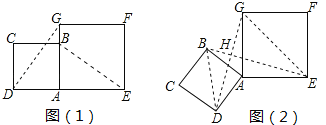 
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于x的方程x2﹣（2m+1）x+m（m+1）=0，
（1）求证：方程总有两个不相等的实数根；
（2）设方程的两根分别为x1、x2，求
的最小值． -
科目： 来源： 题型：
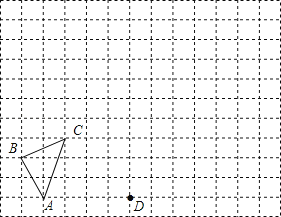
查看答案和解析>>【题目】如图，在由边长为1的单位正方形组成的网格中，按要求画出坐标系及△A1B1C1及△A2B2C2；
（1）若点A、C的坐标分别为（﹣3，0）、（﹣2，3），请画出平面直角坐标系并指出点B的坐标；
（2）画出△ABC关于y轴对称再向上平移1个单位后的图形△A1B1C1；
（3）以图中的点D为位似中心，将△A1B1C1作位似变换且把边长放大到原来的两倍，得到△A2B2C2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，一幢楼房AB背后有一台阶CD，台阶每层高0.2米，且AC＝17.2米，设太阳光线与水平地面的夹角为α，当α＝60°时，测得楼房在地面上的影长AE＝10米，现有一老人坐在MN这层台阶上晒太阳．（
取1.73）（1）求楼房的高度约为多少米？
（2）过了一会儿，当α＝45°时，问老人能否还晒到太阳？请说明理由．
-
科目： 来源： 题型：
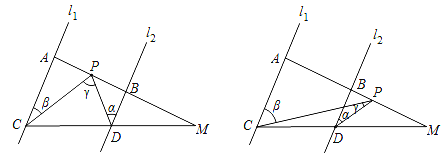
查看答案和解析>>【题目】如图，已知l1∥l2，线段MA分别与直线l1，l2交于点A，B，线段MC分别与直线l1，l2交于点C，D，点P在线段AM上运动（P点与A，B，M三点不重合），设∠PDB＝α，∠PCA＝β，∠CPD＝γ．
（1）若点P在A，B两点之间运动时，若a＝25°，β＝40°，那么γ＝ ．
（2）若点P在A，B两点之间运动时，探究α，β，γ之间的数量关系，请说明理由；
（3）若点P在B，M两点之间运动时，α，β，γ之间有何数量关系？（只需直接写出结论）
相关试题
