【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出四个结论:①b2 > 4ac;②2a+b=0;③a-b+c=0;④5a < b.其中正确结论有( )
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】C
【解析】由函数图象可知b2-4ac>0,故b2>4ac成立,则①正确;由对称轴x=-1知, ![]() ,故2a=b,又因函数图象开口向下知a<0,故2a+b<0,则②错误;由题目可知函数图象与x轴的另一个交点是(1,0),故a+b+c=0,则③正确;由对称轴x=-1知,
,故2a=b,又因函数图象开口向下知a<0,故2a+b<0,则②错误;由题目可知函数图象与x轴的另一个交点是(1,0),故a+b+c=0,则③正确;由对称轴x=-1知, ![]() ,故2a=b,又因函数图象开口向下知a<0,故5a<2a,即5a<b成立,故④正确.
,故2a=b,又因函数图象开口向下知a<0,故5a<2a,即5a<b成立,故④正确.
所以答案是:C.
【考点精析】解答此题的关键在于理解二次函数图象以及系数a、b、c的关系的相关知识,掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E,F分别是矩形ABCD的边BC和CD上的点,其中AB=3
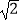 ,BC=3
,BC=3 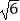 ,把△ABE沿AE进行折叠,使点B落在对角线AC上,在把△ADF沿AF折叠,使点D落在对角线AC上,点P为直线AF上任意一点,则PE的最小值为 .
,把△ABE沿AE进行折叠,使点B落在对角线AC上,在把△ADF沿AF折叠,使点D落在对角线AC上,点P为直线AF上任意一点,则PE的最小值为 . 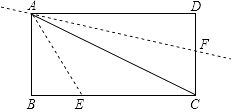
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC,BD为圆O的两条互相垂直的直径,动点P从圆心O出发,沿O→C→D→O的路线作匀速运动,设运动时间为t秒,∠APB的度数为y度,那么表示y与t之间函数关系的图象大致为( )
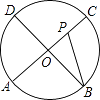
A.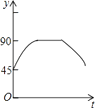
B.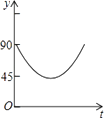
C.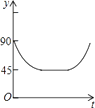
D.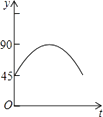
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的,该市自来水收费价格见价目表.
价目表
每月水用量
单价
不超出
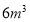 的部分
的部分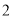 元/
元/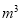
超出
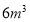 不超出
不超出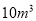 的部分
的部分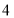 元/
元/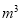
超出
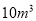 的部分
的部分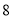 元/
元/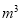
注:水费按月结算.
若某户居民
 月份用水
月份用水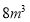 ,则应收水费:
,则应收水费: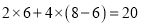 元.
元.(1)若该户居民
 月份用水
月份用水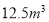 ,则应收水费_______元;
,则应收水费_______元;(2)若该户居民
 、
、 月份共用水
月份共用水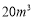 (
(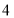 月份用水量超过
月份用水量超过 月份),共交水费
月份),共交水费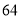 元,则该户居民
元,则该户居民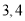 月份各用水多少立方米?
月份各用水多少立方米? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一块塑料矩形模板ABCD,长为10cm,宽为4cm,将你手中足够大的直角三角板 PHF 的直角顶点P落在AD边上(不与A、D重合),在AD上适当移动三角板顶点P:
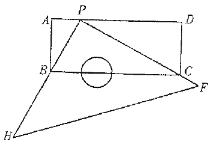
①能否使你的三角板两直角边分别通过点B与点C?若能,请你求出这时 AP 的长;若不能,请说明理由;
②再次移动三角板位置,使三角板顶点P在AD上移动,直角边PH 始终通过点B,另一直角边PF与DC的延长线交于点Q,与BC交于点E,能否使CE=2cm?若能,请你求出这时AP的长;若不能,请你说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:A(0,1),B(2,0),C(4,3)
(1)在直角坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC,BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为7,则GE+FH的最大值为( )
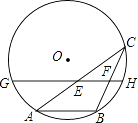
A.10.5
B.7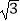 -3.5
-3.5
C.11.5
D.7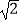 -3.5
-3.5
相关试题

