【题目】如图,点P是⊙O外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D.
(1)求证:PC是⊙O的切线;
(2)若PD=![]() cm,AC=8cm,求图中阴影部分的面积;
cm,AC=8cm,求图中阴影部分的面积;
(3)在(2)的条件下,若点E是弧AB的中点,连接CE,求CE的长.

参考答案:
【答案】(1)证明见解析;
(2)阴影部分的面积为![]() ;
;
(3)CE的长是![]()
【解析】(1)连接OC,证明△PAO≌△PCO,得到∠PAO=∠PCO=90 ,证明结论;
(2)证明△ADO∽△PDA,得到成比例线段求出BC的长,根据S阴=S半⊙O-S△ACB求出答案;
(3)连接AE,BE,过点B作BM⊥CE于点M,分别求出CM和EM的长,求和得到答案.
证明: ⑴如图,连接OC,
∵PA切⊙O于A.
∴∠PAO=90.
∵OP∥BC,
∴∠AOP=∠OBC,∠COP=∠OCB.
∵OC=OB,
∴∠OBC=∠OCB,
∴∠AOP=∠COP.
又∵OA=OC,OP=OP,
∴△PAO≌△PCO (SAS).
∴∠PAO=∠PCO=90 ,
又∵OC是⊙O的半径,
∴PC是⊙O的切线.
⑵解法一:
由(1)得PA,PC都为圆的切线,
∴PA=PC,OP平分∠APC,∠ADO=∠PAO=90 ,
∴∠PAD+∠DAO=∠DAO+∠AOD,
∴∠PAD =∠AOD,
∴△ADO∽△PDA.
∴![]() ,
,
∴![]() ,
,
∵AC=8, PD=![]() ,
,
∴AD=![]() AC=4,OD=3,AO=5,
AC=4,OD=3,AO=5,
由题意知OD为△ABC的中位线,
∴BC=2OD=6,AB=10.
∴S阴=S半⊙O-S△ACB=![]() .
.
答:阴影部分的面积为![]() .
.
解法二:

∵AB是⊙O的直径,OP∥BC,
∴∠PDC=∠ACB=90.
∵∠PCO=90 ,
∴∠PCD+∠ACO=∠ACO+∠OCB=90 ,
即∠PCD=∠OCB.
又∵∠OBC =∠OCB,
∴∠PCD=∠OBC,
∴△PDC∽△ACB,
∴![]() .
.
又∵AC=8, PD=![]() ,
,
∴AD=DC=4,PC=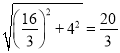 .
.
∴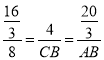 ,
,
∴CB=6,AB=10,
∴S阴=S半⊙O-S△ACB=![]() .
.
答:阴影部分的面积为![]() .
.
(3)如图,连接AE,BE,过点B作BM⊥CE于点M.
∴∠CMB=∠EMB=∠AEB=90,
又∵点E是![]() 的中点,
的中点,
∴∠ECB=∠CBM=∠ABE=45,CM=MB =![]() ,BE=ABcos45=
,BE=ABcos45=![]() ,
,
∴ EM=![]() ,
,
∴CE=CM+EM=![]() .
.
“点睛”本题考查的是切线的判定和性质、扇形面积的计算和相似三角形的判定和性质,灵活运用切线的性质:圆的切线垂直于过切点的半径和切线的判定是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图一根木棒放在数轴上,木棒的左端与数轴上的点A重合,右端与点B重合.
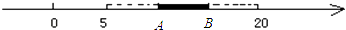
(1)若将木棒沿数轴向右水平移动,则当它的左端移动到B点时,它的右端在数轴上所对应的数为20;若将木棒沿数轴向左水平移动,则当它的右端移动到A点时,则它的左端在数轴上所对应的数为5(单位:cm),由此可得到木棒长为cm.
(2)由题(1)的启发,请你能借助“数轴”这个工具帮助小红解决下列问题:
问题:一天,小红去问曾当过数学老师现在退休在家的爷爷的年龄,爷爷说:“我若是你现在这么大,你还要40年才出生;你若是我现在这么大,我已经125岁,是老寿星了,哈哈!”,请求出爷爷现在多少岁了? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣3﹣(﹣4)+2;
(2)(﹣6)÷2×(﹣ );
);
(3)(﹣ +
+  ﹣
﹣ 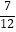 )×(﹣24);
)×(﹣24);
(4)﹣14﹣7÷[2﹣(﹣3)2]. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2+bx+c的图象上有两点(3,4)和(﹣5,4),则此抛物线的对称轴是直线x=
-
科目: 来源: 题型:
查看答案和解析>>【题目】若多项式4a2+M能用平方差公式因式分解,则单项式M=__________.(写出一个即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1,y2(千米)与行驶时间x(小时)之间的函数关系图象.
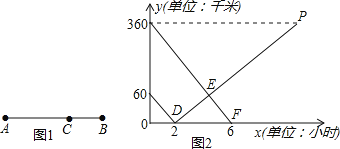
(1)填空:A,B两地相距 千米;
(2)求两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式;
(3)客、货两车何时相遇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下说法正确的是
A. 每个内角都是120°的六边形一定是正六边形.
B. 正n边形的对称轴不一定有n条.
C. 正n边形的每一个外角度数等于它的中心角度数.
D. 正多边形一定既是轴对称图形,又是中心对称图形.
相关试题

