Question

【题目】如图1所示，在A，B两地之间有汽车站C站，客车由A地驶往C站，货车由B地驶往A地．两车同时出发，匀速行驶．图2是客车、货车离C站的路程y1，y2（千米）与行驶时间x（小时）之间的函数关系图象．

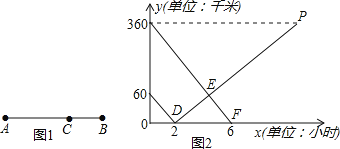
（1）填空：A，B两地相距 千米；

（2）求两小时后，货车离C站的路程y2与行驶时间x之间的函数关系式；

（3）客、货两车何时相遇？

Answer 1

【答案】（1）420；（2）y2=30x﹣60；

【解析】

试题分析：（1）由题意可知：B、C之间的距离为80千米，A、C之间的距离为360千米，所以A，B两地相距360+80=440千米；

（2）根据货车两小时到达C站，求得货车的速度，进一步求得到达A站的时间，进一步设y2与行驶时间x之间的函数关系式可以设x小时到达C站，列出关系式，代入点求得函数解析式即可；

（3）两函数的图象相交，说明两辆车相遇，求得y1的函数解析式，与（2）中的函数解析式联立方程，解决问题．

试题解析：（1）填空：A，B两地相距420千米；

（2）由图可知货车的速度为60÷2=30千米/小时，

货车到达A地一共需要2+360÷30=14小时，

设y2=kx+b，代入点（2，0）、（14，360）得

，

解得，

所以y2=30x﹣60；

（3）设y1=mx+n，代入点（6，0）、（0，360）得

解得，

所以y1=﹣60x+360

由y1=y2得30x﹣60=﹣60x+360

解得x=

答：客、货两车经过小时相遇．