【题目】如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,
∠BAD=45°,AD与BE交于点F,连接CF.
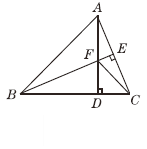
(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.
参考答案:
【答案】(2)2+![]()
【解析】试题分析:(1)先判定出△ABD是等腰直角三角形,根据等腰直角三角形的性质可得AD=BD,再根据同角的余角相等求出∠CAD=∠CBE,然后利用“角边角”证明△ADC和△BDF全等,根据全等三角形对应边相等可得BF=AC,再根据等腰三角形三线合一的性质可得AC=2AE,从而得证;
(2)根据全等三角形对应边相等可得DF=CD,然后利用勾股定理列式求出CF,再根据线段垂直平分线上的点到线段两端点的距离相等可得AF=CF,然后根据AD=AF+DF代入数据即可得解.
(1)证明:∵AD⊥BC,∠BAD=45°,
∴△ABD是等腰直角三角形,
∴AD=BD,
∵BE⊥AC,AD⊥BC
∴∠CAD+∠ACD=90°,
∠CBE+∠ACD=90°,
∴∠CAD=∠CBE,
在△ADC和△BDF中,![]() ,
,
∴△ADC≌△BDF(ASA),
∴BF=AC,
∵AB=BC,BE⊥AC,
∴AC=2AE,
∴BF=2AE;
(2)解:∵△ADC≌△BDF,
∴DF=CD=,
在Rt△CDF中,CF=![]() =
=![]() =2,
=2,
∵BE⊥AC,AE=EC,
∴AF=CF=2,
∴AD=AF+DF=2+.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的格点纸中每个小正方形的边长均为1,以小正方形的顶点为圆心,2为半径做了一个扇形,用该扇形围成一个圆锥的侧面,针对此做法,小明和小亮通过计算得出以下结论:小明说此圆锥的侧面积为
 π;小亮说此圆锥的弧长为
π;小亮说此圆锥的弧长为  π,则下列结论正确的是( )
π,则下列结论正确的是( ) 
A.只有小明对
B.只有小亮对
C.两人都对
D.两人都不对 -
科目: 来源: 题型:
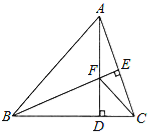
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
(1)求证:AC=AE;
(2)若点E为AB的中点,CD=4,求BE的长.
-
科目: 来源: 题型:
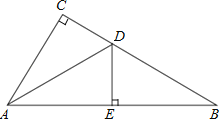
查看答案和解析>>【题目】阅读下面材料: 在数学课上,老师提出如下问题:

小敏的作法如下:
老师说:“小敏的作法正确.”依其作法,先得出ABCD,再得出矩形ABCD,请回答:以上两条结论的依据是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】小华在某月的日历中圈出几个数,算得这三个数的和为36,那么这几个数的形式可能是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,DE⊥BC,垂足为点E,连接CD.
(1)如图1,求DE与BC的数量关系;
(2)如图2,若P是线段CB上一动点(点P不与点B、C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,∠PDF=60°连接BF,请猜想DE、BF、BP三者之间的数量关系,并证明你的结论;


-
科目: 来源: 题型:
查看答案和解析>>【题目】是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题:
(1)汽车在前9分钟内的平均速度是多少?
(2)汽车在中途停了多长时间?
(3)当16≤t≤30时,求S与t的函数关系式.

相关试题

