【题目】如图所示的格点纸中每个小正方形的边长均为1,以小正方形的顶点为圆心,2为半径做了一个扇形,用该扇形围成一个圆锥的侧面,针对此做法,小明和小亮通过计算得出以下结论:小明说此圆锥的侧面积为 ![]() π;小亮说此圆锥的弧长为
π;小亮说此圆锥的弧长为 ![]() π,则下列结论正确的是( )
π,则下列结论正确的是( ) 
A.只有小明对
B.只有小亮对
C.两人都对
D.两人都不对
参考答案:
【答案】C
【解析】解:观察扇形发现:扇形的半径为2,圆心角为150°, ∴扇形的弧长为 ![]() =
= ![]() π;
π;
侧面积为: ![]() =
= ![]() π;
π;
∴两人的说法都正确,
故选C.
【考点精析】掌握弧长计算公式和圆锥的相关计算是解答本题的根本,需要知道若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;圆锥侧面展开图是一个扇形,这个扇形的半径称为圆锥的母线;圆锥侧面积S=πrl;V圆锥=1/3πR2h..
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.

(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正比例函数y=kx与反比例函数y=
 的图象不可能是( )
的图象不可能是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果m、n是两个不相等的实数,且满足
 ,
, ,那么代数式
,那么代数式 ______ .
______ . -
科目: 来源: 题型:
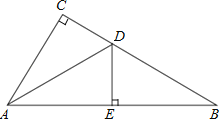
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
(1)求证:AC=AE;
(2)若点E为AB的中点,CD=4,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料: 在数学课上,老师提出如下问题:

小敏的作法如下:
老师说:“小敏的作法正确.”依其作法,先得出ABCD,再得出矩形ABCD,请回答:以上两条结论的依据是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,
∠BAD=45°,AD与BE交于点F,连接CF.
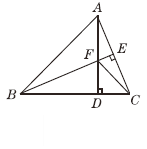
(1)求证:BF=2AE;
(2)若CD=
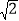 ,求AD的长.
,求AD的长.
相关试题

