【题目】如图,在△ABC中,∠BAC=90°,AB=AC,AD是经过A点的一条直线,且B、C在AD的两侧,BD⊥AD于D,CE⊥AD于E,交AB于点F,CE=10,BD=4,则DE的长为( )

A. 6 B. 5 C. 4 D. 8
参考答案:
【答案】A
【解析】
根据∠BAC=90°,AB=AC,得到∠BAD+∠CAD=90°,由于CE⊥AD于E,于是得到∠ACE+∠CAE=90°,根据余角的性质得到∠BAD=∠ACE,推出△ABD≌△CEA,根据全等三角形的性质即可得到结论.
解:∵∠BAC=90°,AB=AC,
∴∠BAD+∠CAD=90°,
∵CE⊥AD于E,
∴∠ACE+∠CAE=90°,
∴∠BAD=∠ACE,
在△ABD与△ACE中,
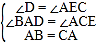 ,
,
∴△ABD≌△CEA(AAS),
∴AE=BD=4,AD=CE=10,
∴DE=AD﹣AE=6.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B、C在同一直线上,
(1)若∠A=∠3,依据__________,可得______∥_______;
(2)若∠______=∠______,则依据内错角相等,两直线平行,可得DB∥EC;
(3)若∠______+∠_______=180°,则AD∥BE,依据是____________;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(﹣3,2),(b,m),(c,m),则点E的坐标是( )
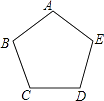
A.(2,﹣3)
B.(2,3)
C.(3,2)
D.(3,﹣2) -
科目: 来源: 题型:
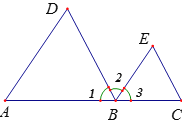
查看答案和解析>>【题目】.如图所示,已知△ABC和△BDE都是等边三角形,下列结论:①AE=CD;②BF=BG;③BH平分∠AHD;④∠AHC=60°;⑤△BFG是等边三角形;⑥FG∥AD,其中正确的有( )

A. 3个 B. 4个 C. 5个 D. 6个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC.∠1=∠3,求证:AB∥DC.
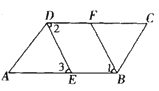
证明:∵∠ABC=∠ADC ( )
∴
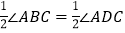 ( )
( )∵BF、DE分别平分∠ABC与∠ADC ( )
∴
 ( )
( )∴∠______=∠______ ( )
∵∠1=∠3( )
∴∠2=∠______ (等量代换)
∴____∥____ ( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知锐角三角形ABC,以点A为圆心,AC为半径画弧与BC交于点E,分别以点E、C为圆心,以大于
 EC的长为半径画弧相交于点P,作射线AP,交BC于点D.若BC=5,AD=4,tan∠BAD=
EC的长为半径画弧相交于点P,作射线AP,交BC于点D.若BC=5,AD=4,tan∠BAD=  ,则AC的长为( )
,则AC的长为( ) 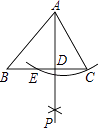
A.3
B.5
C.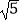
D.2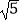
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为2个单位长度/秒,点在弧线上的速度为
 个单位长度/秒,则2017秒时,点P的坐标是( )
个单位长度/秒,则2017秒时,点P的坐标是( ) 
A.(2017,0)
B.(2017,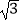 )
)
C.(2017,﹣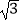 )
)
D.(2016,0)
相关试题

