【题目】在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为2个单位长度/秒,点在弧线上的速度为 ![]() 个单位长度/秒,则2017秒时,点P的坐标是( )
个单位长度/秒,则2017秒时,点P的坐标是( ) 
A.(2017,0)
B.(2017, ![]() )
)
C.(2017,﹣ ![]() )
)
D.(2016,0)
参考答案:
【答案】B
【解析】解:设第n秒运动到Pn(n为自然数)点, 观察,发现规律:P1(1, ![]() ),P2(2,0),P3(3,﹣
),P2(2,0),P3(3,﹣ ![]() ),P4(4,0),P5(5,
),P4(4,0),P5(5, ![]() ),…,
),…,
∴P4n+1(4n+1, ![]() ),P4n+2(4n+2,0),P4n+3(4n+3,﹣
),P4n+2(4n+2,0),P4n+3(4n+3,﹣ ![]() ),P4n+4(4n+4,0).
),P4n+4(4n+4,0).
∵2017=4×504+1,
∴P2017为(2017, ![]() ).
).
故选B.
设第n秒运动到Pn(n为自然数)点,根据点P的运动规律找出部分Pn点的坐标,根据坐标的变化找出变化规律“P4n+1(4n+1, ![]() ),P4n+2(4n+2,0),P4n+3(4n+3,﹣
),P4n+2(4n+2,0),P4n+3(4n+3,﹣ ![]() ),P4n+4(4n+4,0)”,依此规律即可得出结论.
),P4n+4(4n+4,0)”,依此规律即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=AC,AD是经过A点的一条直线,且B、C在AD的两侧,BD⊥AD于D,CE⊥AD于E,交AB于点F,CE=10,BD=4,则DE的长为( )

A. 6 B. 5 C. 4 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC.∠1=∠3,求证:AB∥DC.
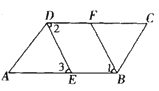
证明:∵∠ABC=∠ADC ( )
∴
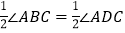 ( )
( )∵BF、DE分别平分∠ABC与∠ADC ( )
∴
 ( )
( )∴∠______=∠______ ( )
∵∠1=∠3( )
∴∠2=∠______ (等量代换)
∴____∥____ ( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知锐角三角形ABC,以点A为圆心,AC为半径画弧与BC交于点E,分别以点E、C为圆心,以大于
 EC的长为半径画弧相交于点P,作射线AP,交BC于点D.若BC=5,AD=4,tan∠BAD=
EC的长为半径画弧相交于点P,作射线AP,交BC于点D.若BC=5,AD=4,tan∠BAD=  ,则AC的长为( )
,则AC的长为( ) 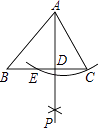
A.3
B.5
C.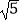
D.2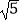
-
科目: 来源: 题型:
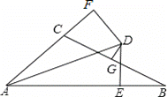
查看答案和解析>>【题目】已知∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB =12,AC =6,则BE= ___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两种型号的机器加工同一种零件,已知A型机器比B型机器每小时多加工20个零件,A型机器加工400个零件所用时间与B型机器加工300个零件所用时间相同.A型机器每小时加工零件的个数_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知经过原点的抛物线y﹣ax2+bx+c(a≠0)的对称轴是直线x=﹣1,下列结论中:①ab>0,②a+b+c>0,③当﹣2<x<0时,y<0,正确的结论是 .
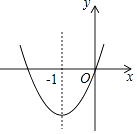
相关试题

