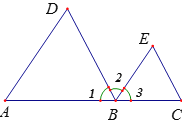
【题目】如图,A、B、C在同一直线上,
(1)若∠A=∠3,依据__________,可得______∥_______;
(2)若∠______=∠______,则依据内错角相等,两直线平行,可得DB∥EC;
(3)若∠______+∠_______=180°,则AD∥BE,依据是____________;
参考答案:
【答案】(1)同位角相等,两直线平行;AD,BE;(2)∠2,∠E;(3)∠A,∠ABE;同旁内角互补,两直线平行.
【解析】
(1)∠A和∠3是同位角,根据同位角相等,两直线平行即可解答;
(2)要利用内错角相等,两直线平行,证明DB∥EC,需要找出一对内错角相等;
(3)要利用同旁内角互补,两直线平行,证明AD∥BE,需要找出一对同旁内角互补的角,据此解答.
(1)若∠A=∠3,依据同位角相等,两直线平行,可得AD∥BE;
(2)若∠2=∠E,则依据内错角相等,两直线平行,可得DB∥EC;
(3)若∠A+∠ABE=180°,则AD∥BE,依据是同旁内角互补,两直线平行;
故答案为:(1)同位角相等,两直线平行;AD,BE;(2)∠2,∠E;(3)∠A,∠ABE;同旁内角互补,两直线平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,DE∥AB.请根据已知条件进行推理,分别得出结论,并在括号内注明理由.

(1)∵DE∥AB,( 已知 )
∴∠2= . ( , )
(2)∵DE∥AB,(已知 )
∴∠3= .( , )
(3)∵DE∥AB(已知 ),
∴∠1+ =180°.( , )
-
科目: 来源: 题型:
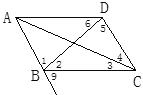
查看答案和解析>>【题目】如图,若∠2=∠6,则____∥___;如果∠BCD+∠ADC=180°,那么____∥____;如果∠9=_____,那么AD∥BC;如果∠9=____,那么AB∥CD;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小学为了了解各年级留守儿童的数量,对一到六年级留守儿童数量进行了统计,得到每个年级的留守儿童人数分别为10,15,10,17,18,20.对于这组数据,下列说法错误的是( )
A.平均数是15
B.众数是10
C.中位数是17
D.方差是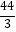
-
科目: 来源: 题型:
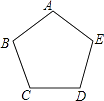
查看答案和解析>>【题目】如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(﹣3,2),(b,m),(c,m),则点E的坐标是( )
A.(2,﹣3)
B.(2,3)
C.(3,2)
D.(3,﹣2) -
科目: 来源: 题型:
查看答案和解析>>【题目】.如图所示,已知△ABC和△BDE都是等边三角形,下列结论:①AE=CD;②BF=BG;③BH平分∠AHD;④∠AHC=60°;⑤△BFG是等边三角形;⑥FG∥AD,其中正确的有( )

A. 3个 B. 4个 C. 5个 D. 6个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=AC,AD是经过A点的一条直线,且B、C在AD的两侧,BD⊥AD于D,CE⊥AD于E,交AB于点F,CE=10,BD=4,则DE的长为( )

A. 6 B. 5 C. 4 D. 8
相关试题

