【题目】(问题)
如图1,在Rt△ABC中,∠ACB=90°,AC=BC,过点C作直线l平行于AB.∠EDF=90°,点D在直线l上移动,角的一边DE始终经过点B,另一边DF与AC交于点P,研究DP和DB的数量关系.

(探究发现)
(1)如图2,某数学兴趣小组运用“从特殊到一般”的数学思想,发现当点D移动到使点P与点C重合时,通过推理就可以得到DP=DB,请写出证明过程;
(数学思考)
(2)如图3,若点P是AC上的任意一点(不含端点A、C),受(1)的启发,这个小组过点D作DG⊥CD交BC于点G,就可以证明DP=DB,请完成证明过程;
(拓展引申)
(3)如图4,在(1)的条件下,M是AB边上任意一点(不含端点A、B),N是射线BD上一点,且AM=BN,连接MN与BC交于点Q,这个数学兴趣小组经过多次取M点反复进行实验,发现点M在某一位置时BQ的值最大.若AC=BC=4,请你直接写出BQ的最大值.
参考答案:
【答案】(1)见解析;(2)见解析;(3)2.
【解析】
(1)由等腰直角三角形的性质可得∠CAB=∠CBA=45°,由平行线的性质可得∠CBA=∠DCB=45°,即可证DB=DP;
【数学思考】
(2)通过证明△CDP≌△GDB,可得DP=DB
【拓展引申】
(3)过点M作MH⊥MN交AC于点H,通过证明△AMH≌△BNQ,可得AH=BQ,通过证明△ACM∽△BMQ,可得![]() ,可得BQ=
,可得BQ=![]() +2,由二次函数的性质可求BQ的最大值.
+2,由二次函数的性质可求BQ的最大值.
(1)∵∠ACB=90°,AC=BC
∴∠CAB=∠CBA=45°
∵CD∥AB
∴∠CBA=∠DCB=45°,且BD⊥CD
∴∠DCB=∠DBC=45°
∴DB=DC
即DB=DP
【数学思考】
(2)∵DG⊥CD,∠DCB=45°
∴∠DCG=∠DGC=45°
∴DC=DG,∠DCP=∠DGB=135°,
∵∠BDP=∠CDG=90°
∴∠CDP=∠BDG,且DC=DG,∠DCP=∠DGB=135°,
∴△CDP≌△GDB(ASA)
∴DB=DP
【拓展引申】
(3)如图4,过点M作MH⊥MN交AC于点H,连接CM,HQ,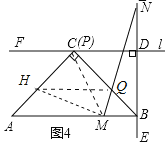
∵MH⊥MN,
∴∠AMH+∠NMB=90°
∵CD∥AB,∠CDB=90°
∴∠DBM=90°
∴∠NMB+∠MNB=90°
∴∠HMA=∠MNB,且AM=BN,∠CAB=∠CBN=45°
∴△AMH≌△BNQ(ASA)
∴AH=BQ
∵∠ACB=90°,AC=BC=4,
∴AB=4![]() ,AC-AH=BC-BQ
,AC-AH=BC-BQ
∴CH=CQ
∴∠CHQ=∠CQH=45°=∠CAB
∴HQ∥AB
∴∠HQM=∠QMB
∵∠ACB=∠HMQ=90°
∴点H,点M,点Q,点C四点共圆,
∴∠HCM=∠HQM
∴∠HCM=∠QMB,且∠A=∠CBA=45°
∴△ACM∽△BMQ
∴![]()
∴![]()
∴BQ=![]() +2
+2
∴AM=2![]() 时,BQ有最大值为2.
时,BQ有最大值为2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

(1)这次统计共抽查了 名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
(4)某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选中同一种沟通方式的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,一次函数
 的图象与y轴交于点A,与反比例函数
的图象与y轴交于点A,与反比例函数 的图象交于点
的图象交于点 .
. ______;
______; ______;
______; 点C是线段AB上的动点
点C是线段AB上的动点 与点A、B不重合
与点A、B不重合 ,过点C且平行于y轴的直线l交这个反比例函数的图象于点D,求
,过点C且平行于y轴的直线l交这个反比例函数的图象于点D,求 面积的最大值;
面积的最大值; 将
将 中面积取得最大值的
中面积取得最大值的 沿射线AB方向平移一定的距离,得到
沿射线AB方向平移一定的距离,得到 ,若点O的对应点
,若点O的对应点 落在该反比例函数图象上
落在该反比例函数图象上 如图
如图 ,则点
,则点 的坐标是______.
的坐标是______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,种植花卉的利润y2与投资量x的平方成正比例关系,并得到了表格中的数据.
投资量x(万元)
2
种植树木利润y1(万元)
4
种植花卉利润y2(万元)
2
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉金额m万元,种植花卉和树木共获利利润W万元,直接写出W关于m的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?
(3)若该专业户想获利不低于22万,在(2)的条件下,直接写出投资种植花卉的金额m的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在我市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,该校有几种购买方案?
(3)上面的哪种方案费用最低?按费用最低方案购买需要多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将长为10的线段OA绕点O旋转
 得到OB,点A的运动轨迹为
得到OB,点A的运动轨迹为 ,P是半径OB上一动点,Q是
,P是半径OB上一动点,Q是 上的一动点,连接PQ.
上的一动点,连接PQ. 当
当 ______度时,PQ有最大值,最大值为______.
______度时,PQ有最大值,最大值为______. 如图2,若P是OB中点,且
如图2,若P是OB中点,且 于点P,求
于点P,求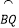 的长;
的长;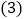 如图3,将扇形AOB沿折痕AP折叠,使点B的对应点
如图3,将扇形AOB沿折痕AP折叠,使点B的对应点 恰好落在OA的延长线上,求阴影部分面积.
恰好落在OA的延长线上,求阴影部分面积. 如图4,将扇形OAB沿PQ折叠,使折叠后的弧
如图4,将扇形OAB沿PQ折叠,使折叠后的弧 恰好与半径OA相切,切点为C,若
恰好与半径OA相切,切点为C,若 ,求点O到折痕PQ的距离.
,求点O到折痕PQ的距离.



-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点
 ,若平移点
,若平移点 到点
到点 ,使以点
,使以点 为顶点的四边形是菱形,则正确的平移方法是( )
为顶点的四边形是菱形,则正确的平移方法是( )
A. 向左平移(
 )个单位,再向上平移1个单位
)个单位,再向上平移1个单位B. 向左平移
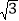 个单位,再向下平移1个单位
个单位,再向下平移1个单位C. 向右平移
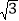 个单位,再向上平移1个单位
个单位,再向上平移1个单位D. 向右平移2个单位,再向上平移1个单位
相关试题

