【题目】如图，在平面直角坐标系中，已知点，若平移点到点，使以点为顶点的四边形是菱形，则正确的平移方法是( )

A. 向左平移（）个单位，再向上平移1个单位

B. 向左平移个单位，再向下平移1个单位

C. 向右平移个单位，再向上平移1个单位

D. 向右平移2个单位，再向上平移1个单位

参考答案：

【答案】C

【解析】分析：过点B作BH⊥OA，交OA于点H，利用勾股定理可求出OB的长，进而可得点A向左或向右平移的距离，由菱形的性质可知BC∥OA，所以可得向上或向下平移的距离，问题得解．

详解：过B作射线BC∥OA，在BC上截取BC=OA，则四边形OACB是平行四边形，

过B作BH⊥x轴于H，

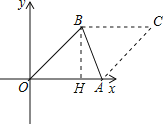
∵B（，1），

∴OB=，

∵A（2，0），

∴C（3，1）

∴OA=OB，

∴则四边形OACB是菱形，

∴平移点A到点C，向右平移个单位，再向上平移1个单位而得到，

故选C．

关闭