【题目】将两块全等的三角板如图①摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.
(1)将图①中的△A1B1C顺时针旋转45°得图②,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;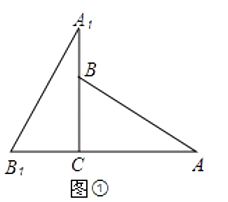
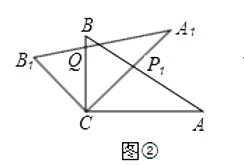
(2)在图②中,若AP1=2,则CQ等于多少?
(3)如图③,在B1C上取一点E,连接BE、P1E,设BC=1,当BE⊥P1B时,求△P1BE面积的最大值.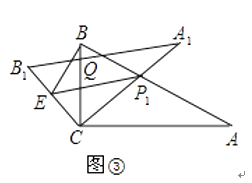
参考答案:
【答案】
(1)证明:∵∠B1CB=45°,∠B1CA1=90°,
∴∠B1CQ=∠BCP1=45°,
∵在△B1CQ和△BCP1中,
 ,
,
∴△B1CQ≌△BCP1(ASA),
∴CQ=CP1
(2)解:作P1D⊥CA于D,
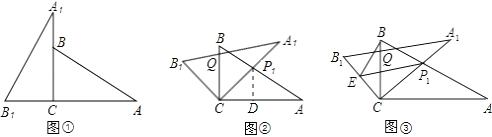
∵∠A=30°,
∴P1D= ![]() AP1=1,
AP1=1,
∵∠P1CD=45°,
∴ ![]() =sin45°=
=sin45°= ![]() ,
,
∴CP1= ![]() P1D=
P1D= ![]() ,
,
又∵CP1=CQ,
∴CQ= ![]()
(3)解:∵∠P1BE=90°,∠ABC=60°,
∴∠A=∠CBE=30°,
∴AC= ![]() BC,
BC,
由旋转的性质可得:∠ACP1=∠BCE,
∴△AP1C∽△BEC,
∴AP1:BE=AC:BC= ![]() :1,
:1,
设AP1=x,则BE= ![]() x,
x,
在Rt△ABC中,∠A=30°,
∴AB=2BC=2,
∴S△P1BE= ![]() ×
× ![]() x(2﹣x)=﹣
x(2﹣x)=﹣ ![]() x2+
x2+ ![]() x
x
=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() ,
,
故当x=1时,S△P1BE(max)= ![]()
【解析】(1)根据旋转的性质,易证得△B1CQ≌△BCP1,即可得到CQ=CP1。
(2)由(1)结论可知CQ=CP1。要求CQ的长,只需求出CP1的长,添加辅助线,将CP1转化到直角三角形中,作P1D⊥CA于D,根据∠A=30°,可求出P1D的长,然后在Rt△P1DC中,可求出CP1的长,即可得出结论。
(3)根据旋转的性质,先证明△AP1C∽△BEC,得对应边成比例,建立方程,用含x的代数式分别表示出AP1、BE的长,在Rt△ABC中,求出AB的长,即可求出S△P1BE与x的函数关系式,求出顶点坐标,即可得到△P1BE面积的最大值。
【考点精析】根据题目的已知条件,利用二次函数的最值和相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小云想用7天的时间背诵若干首诗词,背诵计划如下:
①将诗词分成4组,第i组有
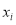 首,i =1,2,3,4;
首,i =1,2,3,4;②对于第i组诗词,第i天背诵第一遍,第(
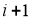 )天背诵第二遍,第(
)天背诵第二遍,第(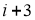 )天背诵第三遍,三遍后完成背诵,其它天无需背诵,
)天背诵第三遍,三遍后完成背诵,其它天无需背诵,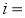 1,2,3,4;
1,2,3,4;第1天
第2天
第3天
第4天
第5天
第6天
第7天
第1组
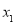
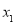
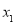
第2组
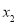
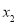
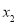
第3组
第4组
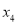
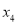
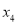
③每天最多背诵14首,最少背诵4首.
解答下列问题:
(1)填入
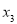 补全上表;
补全上表;(2)若
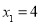 ,
, ,
, ,则
,则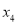 的所有可能取值为______;
的所有可能取值为______;(3)7天后,小云背诵的诗词最多为______首.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,点O为坐标原点,点A(a,0)、B(b,O)分别在x轴正半轴和y轴正半轴上,且
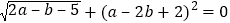 ,点P从原点出发以每秒2个单位长度的速度沿x轴正半轴方向运动.
,点P从原点出发以每秒2个单位长度的速度沿x轴正半轴方向运动.(1)求点A、B的坐标;
(2)连接PB,设三角形ABP的面积为s,点P的运动时间为t,请用含t的式子表示s,并直接写出t的取值范围;
(3)在(2)的条件下,将线段OB沿x轴正方向平移,使点O与点A重合,点B的对应点为点D,连接BD,将线段PB沿x轴正方向平移,使点B与点D重合,点P的对应点为点Q,取DQ的中点H,是否存在t的值,使三角形ABP的面积等于三角形ADH的面积?若存在,求出t的值;若不存在,请说明理由.
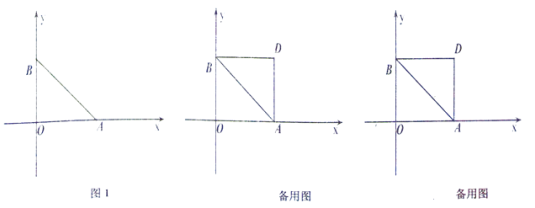
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起(其中,
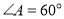 ,
,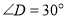 ;
;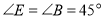 ).
).
(1)①若
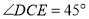 ,则
,则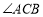 的度数为_____________;
的度数为_____________;②若
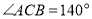 ,则
,则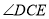 的度数为_____________.
的度数为_____________.(2)由(1)猜想
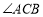 与
与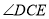 的数量关系,并说明理由.
的数量关系,并说明理由.(3)当
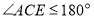 且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出
且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出 角度所有可能的值(不必说明理由);若不存在,请说明理由.
角度所有可能的值(不必说明理由);若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,四边形ABCD是直角梯形,BC∥AD,∠BAD=90°,BC与y轴相交于点M,且M是BC的中点,A,B,D三点的坐标分别是A(﹣1,0),B(﹣l,2),D(3,0).连接DM,并把线段DM沿DA方向平移到ON.若抛物线y=ax2+bx+c经过点D,M,N.
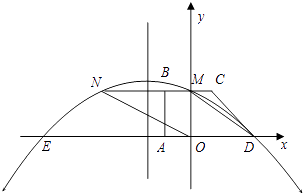
(1)求抛物线的解析式.
(2)抛物线上是否存在点P,使得PA=PC?若存在,求出点P的坐标;若不存在,请说明理由.
(3)设抛物线与x轴的另一个交点为E,点Q是抛物线的对称轴上的一个动点,当点Q在什么位置时有|QE﹣QC|最大?并求出最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某油箱容量为60L的汽车,加满汽油后行驶了100km时,油箱中的汽油大约消耗了
 ,如果加满汽油后汽车行驶的路程为x(km),油箱中剩油量为y(L),则y与x之间的函数解析式和自变量取值范围分别是( )
,如果加满汽油后汽车行驶的路程为x(km),油箱中剩油量为y(L),则y与x之间的函数解析式和自变量取值范围分别是( )A. y=0.12x,x>0
B. y=60-0.12x,x>0
C. y=0.12x,0≤x≤500
D. y=60-0.12x,0≤x≤500
-
科目: 来源: 题型:
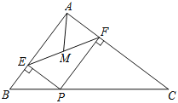
查看答案和解析>>【题目】如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为 ( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

