【题目】小云想用7天的时间背诵若干首诗词,背诵计划如下:
①将诗词分成4组,第i组有![]() 首,i =1,2,3,4;
首,i =1,2,3,4;
②对于第i组诗词,第i天背诵第一遍,第(![]() )天背诵第二遍,第(
)天背诵第二遍,第(![]() )天背诵第三遍,三遍后完成背诵,其它天无需背诵,
)天背诵第三遍,三遍后完成背诵,其它天无需背诵,![]() 1,2,3,4;
1,2,3,4;
第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | |
第1组 |
|
|
| ||||
第2组 |
|
|
| ||||
第3组 | |||||||
第4组 |
|
|
|
③每天最多背诵14首,最少背诵4首.
解答下列问题:
(1)填入![]() 补全上表;
补全上表;
(2)若![]() ,
,![]() ,
,![]() ,则
,则![]() 的所有可能取值为______;
的所有可能取值为______;
(3)7天后,小云背诵的诗词最多为______首.
参考答案:
【答案】(1)如表所示,见解析;(2)4,5,6;(3)23.
【解析】
(1)根据表中的规律即可得到结论;
(2)根据题意列不等式即可得到结论;
(3)根据题意列不等式,即可得到结论.
解:(1)
第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | |
第1组 | x1 | x1 | x1 | ||||
第2组 | x2 | x2 | x2 | ||||
第3组 | x3 | x3 | x3 | ||||
第4组 | x4 | x4 | x4 |
(2)∵每天最多背诵14首,最少背诵4首,
∴x1≥4,x3≥4,x4≥4,
∴x1+x3≥8①,
∵x1+x3+x4≤14②,
把①代入②得,x4≤6,
∴4≤x4≤6,
∴x4的所有可能取值为4,5,6,
故答案为:4,5,6;
(3)∵每天最多背诵14首,最少背诵4首,
∴由第2天,第3天,第4天,第5天得,
x1+x2≤14①,x2+x3≤14②,x1+x3+x4≤14③,x2+x4≤14④,
①+②+④-③得,3x2≤28,
![]() ,
,
![]() ,
,
![]()
∴7天后,小云背诵的诗词最多为23首,
故答案为:23.
-
科目: 来源: 题型:
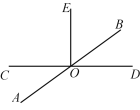
查看答案和解析>>【题目】已知如图,直线
 ,
,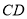 相交于点
相交于点  ,
, .
.
(1)若
 ,求
,求  的度数;
的度数;(2)若
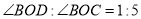 ,求
,求 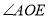 的度数;
的度数;(3)在(
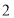 )的条件下,过点
)的条件下,过点  作
作  ,请直接写出
,请直接写出 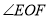 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠ABC的平分线交AC于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB,BC于点E,F.
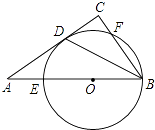
(1)求证:AC是⊙O的切线;
(2)已知AB=5,AC=4,求⊙O的半径r. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某日在我国某岛附近海域有两艘自西向东航行的海监船A、B,船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留小数点后一位)
参考数据: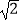 ≈1.414,
≈1.414, 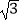 ≈1.732,
≈1.732, 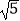 ≈2.236.
≈2.236.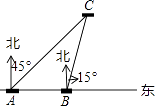
-
科目: 来源: 题型:
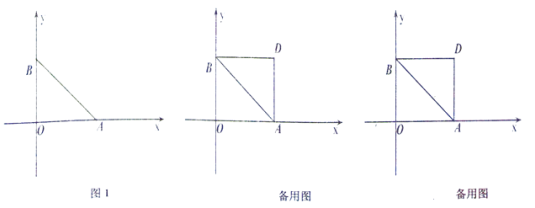
查看答案和解析>>【题目】如图1,在平面直角坐标系中,点O为坐标原点,点A(a,0)、B(b,O)分别在x轴正半轴和y轴正半轴上,且
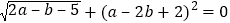 ,点P从原点出发以每秒2个单位长度的速度沿x轴正半轴方向运动.
,点P从原点出发以每秒2个单位长度的速度沿x轴正半轴方向运动.(1)求点A、B的坐标;
(2)连接PB,设三角形ABP的面积为s,点P的运动时间为t,请用含t的式子表示s,并直接写出t的取值范围;
(3)在(2)的条件下,将线段OB沿x轴正方向平移,使点O与点A重合,点B的对应点为点D,连接BD,将线段PB沿x轴正方向平移,使点B与点D重合,点P的对应点为点Q,取DQ的中点H,是否存在t的值,使三角形ABP的面积等于三角形ADH的面积?若存在,求出t的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起(其中,
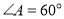 ,
,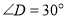 ;
;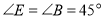 ).
).
(1)①若
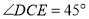 ,则
,则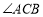 的度数为_____________;
的度数为_____________;②若
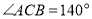 ,则
,则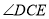 的度数为_____________.
的度数为_____________.(2)由(1)猜想
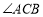 与
与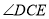 的数量关系,并说明理由.
的数量关系,并说明理由.(3)当
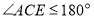 且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出
且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出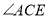 角度所有可能的值(不必说明理由);若不存在,请说明理由.
角度所有可能的值(不必说明理由);若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】将两块全等的三角板如图①摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.
(1)将图①中的△A1B1C顺时针旋转45°得图②,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;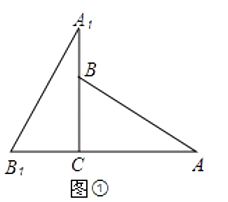
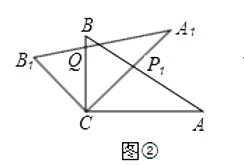
(2)在图②中,若AP1=2,则CQ等于多少?
(3)如图③,在B1C上取一点E,连接BE、P1E,设BC=1,当BE⊥P1B时,求△P1BE面积的最大值.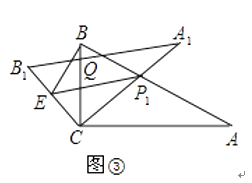
相关试题

