【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起(其中,![]() ,
,![]() ;
;![]() ).
).

(1)①若![]() ,则
,则![]() 的度数为_____________;
的度数为_____________;
②若![]() ,则
,则![]() 的度数为_____________.
的度数为_____________.
(2)由(1)猜想![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(3)当![]() 且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出
且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出![]() 角度所有可能的值(不必说明理由);若不存在,请说明理由.
角度所有可能的值(不必说明理由);若不存在,请说明理由.
参考答案:
【答案】(1)①![]() ;②
;②![]() ;(2)
;(2)![]() ,理由详见解析;(3)∠ACE=45°或30°或120°或135°或165°
,理由详见解析;(3)∠ACE=45°或30°或120°或135°或165°
【解析】
(1)①先求出∠ACE,即可求出∠ACB;
②先求出∠ACE,即可求出∠DCE;
(2)根据题意可得![]() ,
,![]() ,从而求出
,从而求出![]() 与
与![]() 的数量关系;
的数量关系;
(3)根据平行线的判定定理和边的平行关系分类讨论,然后画出对应的图形即可得出结论.
解:(1)①∵![]() ,∠ACD=∠BCE=90°
,∠ACD=∠BCE=90°
∴∠ACE=∠ACD-∠DCE=45°
∴∠ACB=∠ACE+∠BCE=135°
故答案为:![]() .
.
②∵![]() ,∠ACD=∠BCE=90°
,∠ACD=∠BCE=90°
∴∠ACE=∠ACB-∠BCE=50°
∴∠DCE=∠ACD-∠ACE =40°
故答案为:![]() .
.
(2)![]() .理由如下
.理由如下
∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]()
∴![]() .
.
(3)①当![]() 时,
时,
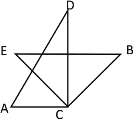
∵![]()
∴![]()
∴![]() ,
,
②当![]() 时,设CE与AD交于点F,如下图所示
时,设CE与AD交于点F,如下图所示
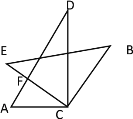
∵∠A=60°,∠BCE=90°
∴∠AFC=180°-∠ACE-∠A=90°
∴∠AFC=∠BCE
∴![]() .
.
③当![]() 时,如下图所示
时,如下图所示

∵∠ACD=90°,∠D=30°
∴∠DCE=∠ACE-∠ACD=30°
∴∠DCE=∠D
∴![]() .
.
④当![]() 时,如下图所示
时,如下图所示
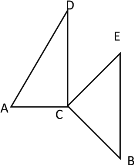
∵∠ACD=90°,∠E=45°
∴∠DCE=∠ACE-∠ACD=45°
∴∠DCE=∠E
∴![]() .
.
⑤当![]() 时,过点C作CG∥AD,如下图所示
时,过点C作CG∥AD,如下图所示
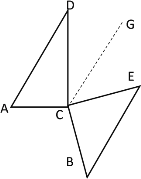
∴∠D=∠DCG=30°
∵∠ACD=90°,∠E=45°
∴∠GCE=∠ACE-∠ACD-∠DCG=45°
∴∠E=∠GCE
∴BE∥CG
∴![]() .
.
综上所述:∠ACE=45°或30°或120°或135°或165°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某日在我国某岛附近海域有两艘自西向东航行的海监船A、B,船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留小数点后一位)
参考数据: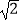 ≈1.414,
≈1.414, 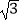 ≈1.732,
≈1.732, 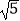 ≈2.236.
≈2.236.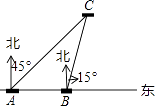
-
科目: 来源: 题型:
查看答案和解析>>【题目】小云想用7天的时间背诵若干首诗词,背诵计划如下:
①将诗词分成4组,第i组有
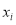 首,i =1,2,3,4;
首,i =1,2,3,4;②对于第i组诗词,第i天背诵第一遍,第(
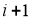 )天背诵第二遍,第(
)天背诵第二遍,第(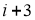 )天背诵第三遍,三遍后完成背诵,其它天无需背诵,
)天背诵第三遍,三遍后完成背诵,其它天无需背诵,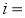 1,2,3,4;
1,2,3,4;第1天
第2天
第3天
第4天
第5天
第6天
第7天
第1组
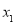
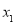
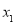
第2组
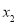
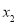
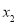
第3组
第4组
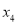
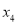
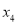
③每天最多背诵14首,最少背诵4首.
解答下列问题:
(1)填入
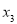 补全上表;
补全上表;(2)若
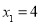 ,
, ,
, ,则
,则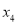 的所有可能取值为______;
的所有可能取值为______;(3)7天后,小云背诵的诗词最多为______首.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,点O为坐标原点,点A(a,0)、B(b,O)分别在x轴正半轴和y轴正半轴上,且
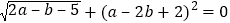 ,点P从原点出发以每秒2个单位长度的速度沿x轴正半轴方向运动.
,点P从原点出发以每秒2个单位长度的速度沿x轴正半轴方向运动.(1)求点A、B的坐标;
(2)连接PB,设三角形ABP的面积为s,点P的运动时间为t,请用含t的式子表示s,并直接写出t的取值范围;
(3)在(2)的条件下,将线段OB沿x轴正方向平移,使点O与点A重合,点B的对应点为点D,连接BD,将线段PB沿x轴正方向平移,使点B与点D重合,点P的对应点为点Q,取DQ的中点H,是否存在t的值,使三角形ABP的面积等于三角形ADH的面积?若存在,求出t的值;若不存在,请说明理由.
-
科目: 来源: 题型:
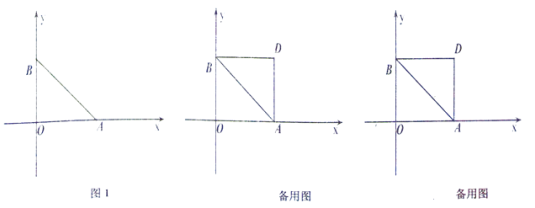
查看答案和解析>>【题目】将两块全等的三角板如图①摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.
(1)将图①中的△A1B1C顺时针旋转45°得图②,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;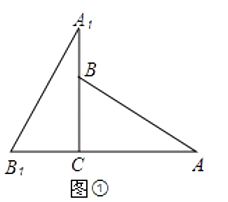
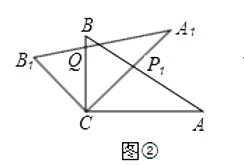
(2)在图②中,若AP1=2,则CQ等于多少?
(3)如图③,在B1C上取一点E,连接BE、P1E,设BC=1,当BE⊥P1B时,求△P1BE面积的最大值.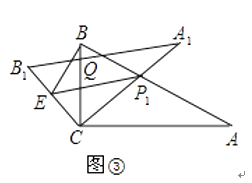
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,四边形ABCD是直角梯形,BC∥AD,∠BAD=90°,BC与y轴相交于点M,且M是BC的中点,A,B,D三点的坐标分别是A(﹣1,0),B(﹣l,2),D(3,0).连接DM,并把线段DM沿DA方向平移到ON.若抛物线y=ax2+bx+c经过点D,M,N.
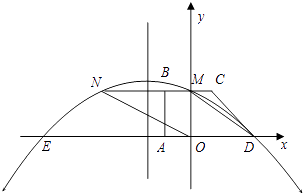
(1)求抛物线的解析式.
(2)抛物线上是否存在点P,使得PA=PC?若存在,求出点P的坐标;若不存在,请说明理由.
(3)设抛物线与x轴的另一个交点为E,点Q是抛物线的对称轴上的一个动点,当点Q在什么位置时有|QE﹣QC|最大?并求出最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某油箱容量为60L的汽车,加满汽油后行驶了100km时,油箱中的汽油大约消耗了
 ,如果加满汽油后汽车行驶的路程为x(km),油箱中剩油量为y(L),则y与x之间的函数解析式和自变量取值范围分别是( )
,如果加满汽油后汽车行驶的路程为x(km),油箱中剩油量为y(L),则y与x之间的函数解析式和自变量取值范围分别是( )A. y=0.12x,x>0
B. y=60-0.12x,x>0
C. y=0.12x,0≤x≤500
D. y=60-0.12x,0≤x≤500
相关试题

