【题目】如图是![]() 的网格图,请根据要求在网格中完成如下任务:
的网格图,请根据要求在网格中完成如下任务:
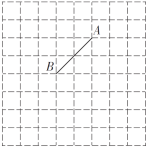
(1)请在网格中建立平面直角坐标系,使点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ;(要求:画出
;(要求:画出![]() 轴、
轴、![]() 轴,并标出
轴,并标出![]() 、
、![]() 和原点
和原点![]() )
)
(2)以![]() 为一边,在网格中作等腰直角三角形
为一边,在网格中作等腰直角三角形![]() ,找出所有符合条件的
,找出所有符合条件的![]() 点,用
点,用![]() 、
、![]() ……表示,并写出它们的坐标.
……表示,并写出它们的坐标.
参考答案:
【答案】(1)见解析;(2)见解析,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
(1)根据点A的坐标,找到坐标原点的位置,然后建立直角坐标系即可;
(2)根据等腰直角三角形腰的情况分类讨论,分别画出对应的图形,即可求出符合要求的点C的坐标.
(1)根据点![]() 坐标为
坐标为![]() ,向下移动2个单位,找到坐标原点O的位置,画出
,向下移动2个单位,找到坐标原点O的位置,画出![]() 轴、
轴、![]() 轴,并标出
轴,并标出![]() 、
、![]() 和原点
和原点![]() ,如下图所示,平面直角坐标系即为所求.
,如下图所示,平面直角坐标系即为所求.
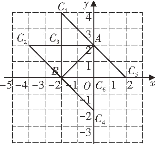
(2)①当等腰直角三角形![]() 是以AC、AB为腰时,如图所示
是以AC、AB为腰时,如图所示
根据勾股定理AC1=AB=![]() ,∠BAC1=45°+45°=90°
,∠BAC1=45°+45°=90°
∴C1符合题意,且![]() ;
;
同理C5符合题意,且![]() ;
;
②当等腰直角三角形![]() 是以BC、BA为腰时,如图所示
是以BC、BA为腰时,如图所示
原理同上:点C2、C4均符合题意,![]() 、
、![]() ;
;
③当等腰直角三角形![]() 是以C为顶点,AC和BC为腰时,如图所示
是以C为顶点,AC和BC为腰时,如图所示
AC3= BC3=2,∠BC3A=90°,
∴C3符合题意,且![]() ;
;
同理C6符合题意,且![]() .
.
综上:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(
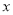 表示时间,
表示时间,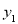 、
、 表示路程),根据图象解答下列问题:
表示路程),根据图象解答下列问题: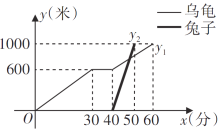
(1)“龟兔再次赛跑”的路程为__________米;
(2)它们两个约定__________先出发(填“兔子”和“乌龟”),先出发__________分钟;
(3)乌龟跑完全程用了__________分钟,兔子跑完全程用了__________分钟,乌龟平均速度是__________米/分,兔子平均速度是__________米/分;
(4)观察图象,你还能得出什么结论?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=x+4的图象与反比例函数y=
 (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.(1)求此反比例函数的表达式;
(2)若点P在x轴上,且S△ACP=
 S△BOC,求点P的坐标.
S△BOC,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个长方形的周长是24厘米,它的一边长是
 (单位:厘米),面积是
(单位:厘米),面积是 (单位:平方厘米).
(单位:平方厘米).(1)若
 ,则这个长方形的面积是__________平方厘米;
,则这个长方形的面积是__________平方厘米;(2)写出
 与
与 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值范围;
的取值范围;(3)画出
 关于
关于 的函数图象.
的函数图象. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司计划在规定时间内生产5G手机24000部,若每天比原计划多生产30部,则在规定时间内可以多生产300部.
(1)求原计划每天生产手机多少部?规定的天数是多少天?
(2)为了提前完成生产任务,公司在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线同时进行生产,已知每组机器人生产流水线每天生产手机的部数与20个工人原计划每天生产的手机总数相同,按此测算,恰好提前两天完成24000部5G手机的生产任务,求原计划安排的工人人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
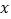 的一元二次方程x2-(k+2)x+k-1=0
的一元二次方程x2-(k+2)x+k-1=0(1)若方程的一个根为 -1,求
 的值和方程的另一个根;
的值和方程的另一个根;(2)求证:不论
 取何值,该方程都有两个不相等的实数根.
取何值,该方程都有两个不相等的实数根. -
科目: 来源: 题型:
查看答案和解析>>【题目】某天猫店销售某种规格学生软式排球,成本为每个30元.以往销售大数据分析表明:当每只售价为40元时,平均每月售出600个;若售价每上涨1元,其月销售量就减少20个,若售价每下降1元,其月销售量就增加200个.
(1)若售价上涨m元,每月能售出 个排球(用m的代数式表示).
(2)为迎接“双十一”,该天猫店在10月底备货1300个该规格的排球,并决定整个11月份进行降价促销,问售价定为多少元时,能使11月份这种规格排球获利恰好为8400元.
相关试题

