【题目】探究题
(1)问题发现
如图1,△ABC和△BDE均为等边三角形,点A,D,E在同一直线上,连接CD.填空;
①CDB的度数为;
②线段AE,CD之间的数量关系为 .
(2)拓展探究
如图2,△ABC和△DBE均为等腰直角三角形,∠ABC=∠DBE=90°,点A,D,E在同一直线上,BF为△DBE中DE边上的高,连接CD.
①求∠CDB的大小;
②请判断线段BF,AD,CD之间的数量关系,并说明理由.
(3)解决问题
如图3,在正方形ABCD中,AC=2 ![]() ,AE=1,CE⊥AE于E,请补全图形,求点B到CE的距离.
,AE=1,CE⊥AE于E,请补全图形,求点B到CE的距离.
参考答案:
【答案】
(1)60°;AE=CD
(2)
解:∠CDB=45°,CD=AD+2BF
理由:∵△ACB和△DBE均为等腰直角三角形,
∴BA=CB,BD=BE,∠ABC=∠DBE=90°.
∴∠ABE=∠CBD.
在△BCD和△BAE中,
∵AB=BC,∠ABE=∠CBD,BD=BE,
∴△BCD≌△BAE(SAS),
∴∠CDB=∠AEB,CD=AE
∵BF是△DBE均为等腰直角三角形,
∴∠CDB=∠AEB=45,DE=2BF,
∴CD=AE=AD+DE=AD+2BF.
∴∠CDB=45°,CD=AD+2BF
(3)
解:①如图,

连接EB,ED,作BH⊥CE,BP⊥BE,
∵四边形ABCD是正方形,
∴∠BAC=45°,AB=AD=CD=BC=2,∠ABC=90°,
∴CD=2,
∴AC=2 ![]() ,
,
∵AE=1,
∴CE= ![]() ,
,
∵A,E,B,C四点共圆,
∴∠BCE=∠CAB=45°,
∴△PBE是等腰直角三角形,
∵△ABC是等腰直角三角形,且C,E,P共线,BH⊥CE,
∴由(2)的结论可得,CE=AE+2BH,
∴ ![]() =2BH+1,
=2BH+1,
∴BH= ![]() .
.
②同①的方法可得,CE=2BH﹣AE,
∴ ![]() =2BH﹣1,
=2BH﹣1,
∴BH= ![]() ,
,
∴点B到CE的距离为 ![]() 或
或 ![]()
【解析】解:(1)①∵△ACB和△DBE均为等边三角形,
∴BA=CB,BD=BE,∠ABC=∠DBE=60°.
∴∠ABE=∠CBD.
在△BCD和△BAE中,
∵AB=BC,∠ABE=∠CBD,BD=BE,
∴△BCD≌△BAE(SAS),
∴∠CDB=∠BEA.
∵△DBE为等边三角形,
∴∠CDB=∠BED=60°.
所以答案是:60°.
②∵△BCD≌△BAE,
∴CD=AE,
所以答案是:CD=AE,
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:
①两边和其中一边的对角对应相等的两个三角形全等.
②角的对称轴是角平分线
③两边对应相等的两直角三角形全等
④成轴对称的两图形一定全等
⑤到线段两端距离相等的点在线段的垂直平分线上,
正确的有
 个.
个.A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司开发出一种高科技电子节能产品,投资2500万元一次性购买整套生产设备,此外生产每件产品需成本20元,每年还需投入500万广告费,按规定该产品的售价不得低于30元/件且不得高于70元/件,该产品的年销售量y(万件)与售价x(元/件)之间的函数关系如下表:
x(元/件)
30
31
…
70
y(万件)
120
119
…
80
(1)求y与x的函数关系式,并写出x的取值范围;
(2)第一年公司是盈利还是亏损?冰球出当盈利最大或亏损最小时该产品的售价;
(3)在(2)的前提下,即在第一年盈利最大或亏损最小时,第二年公司重新确定产品定价,能否使两年盈利3500万元?若能,求第二年产品的售价;若不能,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C.△ABC中,∠A=50°,求∠DBA+∠DCA的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°,试说明:∠GDC=∠B.请补充说明过程,并在括号内填上相应的理由.
解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90° ,
∴EF∥AD( ),
∴ +∠2=180°( ).
又∵∠2+∠3=180°(已知),
∴∠1=∠3( ),
∴AB∥ ( ),
∴∠GDC=∠B( ).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=6,BC=10,AB的垂直平分线分别交BC、AB于点D、E.
(1)求△ACD的周长;
(2)若∠C=25°,求∠CAD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】三角板是学习数学的重要工具,将一副三角板中的两块直角三角板的直角顶点
 按如图方式叠放在一起,当
按如图方式叠放在一起,当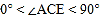 且点
且点 在直线
在直线 的上方时,解决下列问题:(友情提示:
的上方时,解决下列问题:(友情提示: ,
, ,
, .
.
(1)①若
 ,则
,则 的度数为 ;
的度数为 ;②若
 ,则
,则 的度数为 ;
的度数为 ;(2)由(1)猜想
 与
与 的数量关系,并说明理由.
的数量关系,并说明理由.(3)这两块三角板是否存在一组边互相平行?若存在,请直接写出
 的角度所有可能的值(不必说明理由);若不存在,请说明理由.
的角度所有可能的值(不必说明理由);若不存在,请说明理由.
相关试题

