搜索
【题目】如图，在△ABC中，AB=AC=6，BC=10，AB的垂直平分线分别交BC、AB于点D、E．
（1）求△ACD的周长；
（2）若∠C=25°，求∠CAD的度数．
参考答案：
【答案】（1）16；（2）∠CAD=105°．
【解析】
试题（1）根据线段垂直平分线的性质可得AD=BD，所以△ACD的周长=AC+CD+AD=AC+CD+BD=AC+BC=16；（2）由AB=AC，∠C=25°，可得∠B=∠C=25°，∠BAC=130°，再由AD=BD，可得∠BAD=∠B=25°，所以∠CAD=130°-25°=105°．
试题解析：（1）
DE是AB的垂直平分线
AD=BD
△ACD的周长=AC+CD+AD=AC+CD+BD=AC+BC=16；
（2）AB=AC
∠B=∠C=25°，
∠BAC=130°
AD=BD
∠BAD=∠B=25°
∠CAD=130°-25°=105°
-
科目： 来源： 题型：
查看答案和解析>>【题目】有一块直角三角板DEF放置在△ABC上，三角板DEF的两条直角边DE、DF恰好分别经过点B、C．△ABC中，∠A=50°，求∠DBA+∠DCA的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】探究题
（1）问题发现
如图1，△ABC和△BDE均为等边三角形，点A，D，E在同一直线上，连接CD．填空；
①CDB的度数为；
②线段AE，CD之间的数量关系为 ．
（2）拓展探究
如图2，△ABC和△DBE均为等腰直角三角形，∠ABC=∠DBE=90°，点A，D，E在同一直线上，BF为△DBE中DE边上的高，连接CD．
①求∠CDB的大小；
②请判断线段BF，AD，CD之间的数量关系，并说明理由．
（3）解决问题
如图3，在正方形ABCD中，AC=2
，AE=1，CE⊥AE于E，请补全图形，求点B到CE的距离． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知AD⊥BC，EF⊥BC，垂足分别为D、F，∠2+∠3＝180°，试说明：∠GDC＝∠B．请补充说明过程，并在括号内填上相应的理由．
解：∵AD⊥BC，EF⊥BC（已知）
∴∠ADB＝∠EFB＝90° ，
∴EF∥AD（ ），
∴ +∠2＝180°（ ）．
又∵∠2+∠3＝180°（已知），
∴∠1＝∠3（ ），
∴AB∥ （ ），
∴∠GDC＝∠B（ ）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】三角板是学习数学的重要工具，将一副三角板中的两块直角三角板的直角顶点
按如图方式叠放在一起，当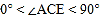
且点
在直线
的上方时，解决下列问题：（友情提示：
，
，
．
（1）①若
，则
的度数为 ；②若
，则
的度数为 ；（2）由（1）猜想
与的数量关系，并说明理由．（3）这两块三角板是否存在一组边互相平行？若存在，请直接写出
的角度所有可能的值（不必说明理由）；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，二次函数y=
x2+bx+c与一次函数y= x﹣3的图象都经过x轴上点A（4，0）和y轴上点B（0，﹣3），过动点M（m，0）（0＜m＜4）作x轴的垂线交直线AB于点C，交抛物线于点P．
（1）求b，c的值；
（2）点M在运动的过程中，能否使△PBC为直角三角形？如果能，求出点P的坐标；如果不能，请说明理由；
（3）如图2，过点P作PD⊥AB于点，设△PCD的面积为S1 ， △ACM的面积为2 ， 若
= 
，
①求m的值；
②如图3，将线段OM绕点O顺时针旋转得到OM′，旋转角为α（0°＜α＜90°），连接M'A、M'B，求M'A+
M'B的最小值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，D是等边三角形ABC内一点，将线段AD绕点A顺时针旋转60°，得到线段AE，连接CD，BE．
（1）求证：∠AEB=∠ADC；
（2）连接DE，若∠ADC=105°，求∠BED的度数．
相关试题
