【题目】为了了解某校学生的身高状况,随机对该校男生、女生的身高进行抽样调查.已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制如图所示的统计图表.

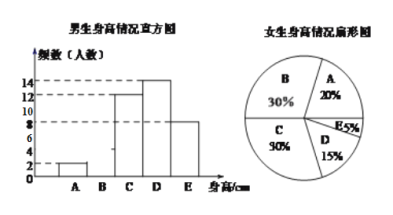
已知女生身高在A组的有8人,根据图表中提供的信息,回答下列问题:
(1)补充图中的男生身高情况直方图,男生身高的中位数落在_______组(填组别字母序号);
(2)在样本中,身高在150≤x<155之间的人数共有_______人,身高人数最多的在____组(填组别序号);
(3)已知该校共有男生400人,女生420人,请估计身高不足160的学生约有多少人?
参考答案:
【答案】(1)补充直方图见解析,D;(2)(2)16,C;(3)估计身高不足160的学生约有516人
【解析】
(1)利用女生身高在A组的人数除以所占百分比计算出女生的总人数即为男生的总人数,用总人数减去A、C、D、E的人数求出B组的人数,即可补全条形图;根据中位数的定义即可得出男生身高的中位数落在D组;
(2)将位于这一小组内的频数相加即可求得结果;
(3)分别用样本中男女生身高不足160的百分比乘以男女生的人数,相加即可得解.
解:(1)女生身高在A组的有8人,所占的百分比为20%,
所以女生的总人数为:8÷20%=40人,
所以男生总人数也为40人,
所以男生身高在B组的有:40-2-12-14-8=4人,
补全条形图如图所示:
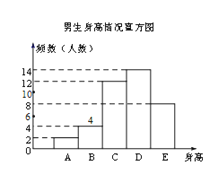
∵男生总人数为40人,
∴中位数是第20和第21人的平均数,
∴男生身高的中位数落在D组;
(2)在样本中,身高在150≤x<155之间的人数共有4+12=16人,身高人数最多的在C组,
故答案为:16、C;
(3)400×![]() +420×(20%+30%+30%)=516.
+420×(20%+30%+30%)=516.
答:估计身高不足160的学生约有516人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两直线l1 , l2分别经过点A(1,0),点B(﹣3,0),并且当两直线同时相交于y正半轴的点C时,恰好有l1⊥l2 , 经过点A、B、C的抛物线的对称轴与直线l1交于点K,如图所示.
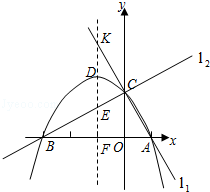
(1)求点C的坐标,并求出抛物线的函数解析式;
(2)抛物线的对称轴被直线l1 , 抛物线,直线l2和x轴依次截得三条线段,问这三条线段有何数量关系?请说明理由;
(3)当直线l2绕点C旋转时,与抛物线的另一个交点为M,请找出使△MCK为等腰三角形的点M,简述理由,并写出点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】“幸福是奋斗出来的”,在数轴上,若C到A的距离刚好是3,则C点叫做A的“幸福点”,若C到A、B的距离之和为6,则C叫做A、B的“幸福中心”
(1)如图1,点A表示的数为﹣1,则A的幸福点C所表示的数应该是 ;
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2,点C就是M、N的幸福中心,则C所表示的数可以是 (填一个即可);
(3)如图3,A、B、P为数轴上三点,点A所表示的数为﹣1,点B所表示的数为4,点P所表示的数为8,现有一只电子蚂蚁从点P出发,以2个单位每秒的速度向左运动,当经过多少秒时,电子蚂蚁是A和B的幸福中心?

-
科目: 来源: 题型:
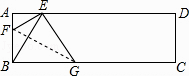
查看答案和解析>>【题目】如图,将矩形纸片ABCD中折叠,使顶点B落在边AD的E点上折痕FG交BC于G,交AB于F,若∠AEF=20°,则∠FGB的度数为( )
A.25°
B.30°
C.35°
D.40° -
科目: 来源: 题型:
查看答案和解析>>【题目】某单位若干名职工参加普法知识竞赛,将成绩制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些职工成绩的中位数和平均数分别是( )

A.94分,96分
B.96分,96分
C.94分,96.4分
D.96分,96.4分 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E、F是AC上的点,判断下列说法错误的是( )
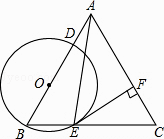
A.若EF⊥AC,则EF是⊙O的切线
B.若EF是⊙O的切线,则EF⊥AC
C.若BE=EC,则AC是⊙O的切线
D.若BE=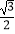 EC,则AC是⊙O的切线
EC,则AC是⊙O的切线 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在扇形BAD中,点C在
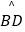 上,且∠BDC=30°,AB=2
上,且∠BDC=30°,AB=2 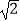 ,∠BAD=105°,过点C作CE⊥AD,则图中阴影部分的面积为( )
,∠BAD=105°,过点C作CE⊥AD,则图中阴影部分的面积为( ) 
A.π﹣2
B.π﹣1
C.2π﹣2
D.2π+1
相关试题

