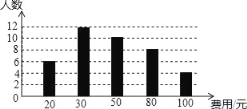
【题目】在全民读书月活动中,某校随机调查了40名同学,本学期计划购买课外书的费用情况,并将结果绘制成如图所示的统计图.根据相关信息,解答下列问题,直接写出结果.
(1)这次调查获取的样本数据的众数是 .
(2)这次调查获取的样本数据的中位数是 .
(3)若该校共有1200名学生,根据样本数据,估计本学期计划购买课外书花费50元的学生有 人.
参考答案:
【答案】(1)40元;(2)50元;(3)300.
【解析】
(1)众数就是出现次数最多的数,据此即可判断;
(2)中位数就是大小处于中间位置的数,根据定义判断;
(3)求得调查的总人数,然后利用1200乘以本学期计划购买课外书花费50元的学生所占的比例即可求解.
(1)这次调查获取的样本数据的众数是40元;
(2)这次调查获取的样本数据的中位数是50元;
(3)调查的总人数是:6+12+10+8+4=40(人),
则估计本学期计划购买课外书花费50元的学生有:1200×![]() =300(人)
=300(人)
故答案为:(1)40元;(2)50元;(3)300.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直径为10的半圆O,tan∠DBC=
 ,∠BCD的平分线交⊙O于F,E为CF延长线上一点,且∠EBF=∠GBF.
,∠BCD的平分线交⊙O于F,E为CF延长线上一点,且∠EBF=∠GBF.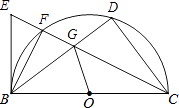
(1)求证:BE为⊙O切线;
(2)求证:BG2=FGCE;
(3)求OG的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,已知点 A(a+b,2-a)与点B(a-5,b-2a)关于y轴对称.
(1)求A、B两点的坐标;
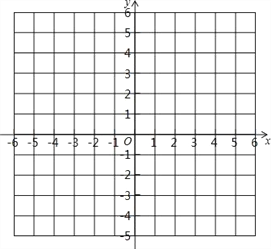
(2)如果点B关于x轴的对称点是C,在图中标出点A、B、C,并求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2﹣x+4与x轴交于点A,B,B点的坐标为(﹣4,0),与y轴交于点C.
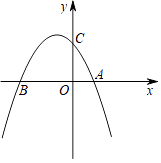
(1)求抛物线的解析式和对称轴.
(2)连接AC、BC,在x轴下方的抛物线上求一点M,使△ABM与△ABC的面积相等.
(3)在x轴下方作平行于x轴的直线l,与抛物线交于点D、E两点(点D在对称轴的左侧).过点D、E分别作x轴的垂线,垂足分别为G、F,当矩形DEFG中DE=2DG时,求D点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】问题探究:
(1)如图①,点M、N分别为四边形ABCD边AD、BC的中点,则四边形BNDM的面积与四边形ABCD的面积关系是 .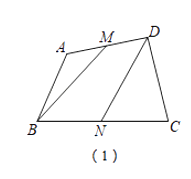
(2)如图②,在四边形ABCD中,点M、N分别为AD、BC的中点,MB交AN于点P,MC交DN于点Q,若S△四边形MPNQ=10,则S△ABP+S△DCQ的值为多少?
(3)问题解决
在矩形ABCD中,AD=2,DC=4,点M、N为AB上两点,且满足BN=2AM=2MN,连接MC、MD.若点P为CD上任意一点,连接AP、NP,使得AP与DM交于点E,NP与MC交于点F,则四边形MEPF的面积是否存最大值?若存在,请求出最大面积;若不存在,请说明理由.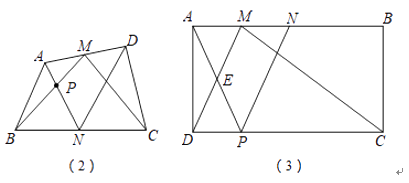
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=10,AC=8,BC=6,DE是AC的垂直平分线,DE交AB于点D,交AC于点E,连接CD,则CD=( )

A.3
B.4
C.4.8
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列算式:
第1个式子:
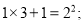
第2个式子:
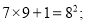
第3个式子:
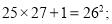
第4个式子:


(1)可猜想第7个等式为 .
(2)探索规律,若字母
 表示自然数,请写出第
表示自然数,请写出第 个等式 .
个等式 . (3)试证明你写出的等式的正确性.
相关试题

