【题目】如图,直径为10的半圆O,tan∠DBC= ![]() ,∠BCD的平分线交⊙O于F,E为CF延长线上一点,且∠EBF=∠GBF.
,∠BCD的平分线交⊙O于F,E为CF延长线上一点,且∠EBF=∠GBF.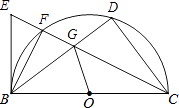
(1)求证:BE为⊙O切线;
(2)求证:BG2=FGCE;
(3)求OG的值.
参考答案:
【答案】
(1)证明:由同弧所对的圆周角相等得∠FBD=∠DCF,
又∵CF平分∠BCD,
∴∠BCF=∠DCF,
已知∠EBF=∠GBF,
∴∠EBF=∠∠BCF,
∵BC为⊙O直径,
∴∠BFC=90°,
∴∠FBC+∠FCB=90°,
∴∠FBC+∠EBF=90°,
∴BE⊥BC,
∴BE为⊙O切线
(2)证明:由(1)知∠BFC=∠EBC=90°,∠EBF=∠ECB,
∴△BEF∽△CEB,
∴BE2=EFCE,
又∠EBF=∠GBF,BF⊥EG,
∴∠BFE=∠BFG=90°,
在△BEF与△BGF中, 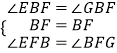 ,
,
∴△BEF≌△BGF,
∴BE=BG,EF=FG,
∴BG2=FGCE
(3)解:如图,过G作GH⊥BC于H, 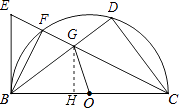
∵CF平分∠BCD,
∴GH=GD,
∵tan∠DBC= ![]() ,
,
∴sin∠DBC= ![]() ,
,
∵BC=10,
∴BD=8,BG=BD﹣GD=8﹣GD,
∴ ![]() =
= ![]() ,
,
∴GD=GH=3,BG=5,BH=4,
∵BC=10,∴OH=OB﹣BH=1,
在Rt△OGH中,由勾股定理得OG= ![]() .
.
【解析】(1)首先依据圆周角定理得到∠FBD=∠DCF,结合角平分线的定义可证明∠EBF=∠∠BCF,故此可得到BE⊥BC;
(2)由(1)知∠BFC=∠EBC=90°,∠EBF=∠ECB,然后依据相似三角形的性质得到BE2=EFCE,得到∠BFE=∠BFG=90°,故此可证明△BEF≌△BGF,根据全等三角形的性质得到BE=BG,EF=FG,最后,通过等量代换可得到问题的答案;
(3)过G作GH⊥BC于H,首先依据角平分线的性质得到GH=GD,接下来,在依据三角函数的定义得到![]() =
=![]() =
=![]() 从而可求得DG的长,最后,在依据勾股定理求解即可.
从而可求得DG的长,最后,在依据勾股定理求解即可.
【考点精析】利用切线的判定定理和相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
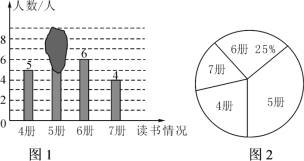
查看答案和解析>>【题目】老师随机抽查了本学期学生读课外书册数的情况,绘制成条形统计图(如图1)和不完整的扇形图(如图2),其中条形统计图被墨迹遮盖了一部分.
(1)求条形统计图中被遮盖的数,并写出册数的中位数;
(2)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没有改变,则最多补查了____人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,点A(0,0)、B(4
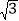 ,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第2017个等边三角形的边长等于( )
,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第2017个等边三角形的边长等于( )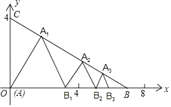
A.
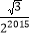 B.
B. 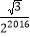 C.
C. 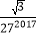 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,AD∥BC,∠BAD的平分线交BC于点G,∠BCD=90°.
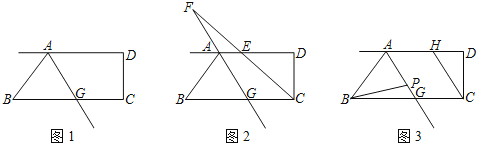
(1)求证:∠BAG=∠BGA;
(2)如图2,若∠ABG=50°,∠BCD的平分线交AD于点E、交射线GA于点F.求∠AFC的度数;
(3)如图3,线段AG上有一点P,满足∠ABP=3∠PBG,过点C作CH∥AG.若在直线AG上取一点M,使∠PBM=∠DCH,请直接写出
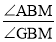 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,已知点 A(a+b,2-a)与点B(a-5,b-2a)关于y轴对称.
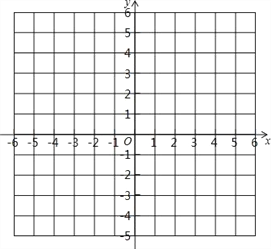
(1)求A、B两点的坐标;
(2)如果点B关于x轴的对称点是C,在图中标出点A、B、C,并求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2﹣x+4与x轴交于点A,B,B点的坐标为(﹣4,0),与y轴交于点C.
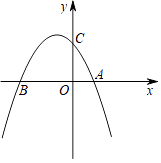
(1)求抛物线的解析式和对称轴.
(2)连接AC、BC,在x轴下方的抛物线上求一点M,使△ABM与△ABC的面积相等.
(3)在x轴下方作平行于x轴的直线l,与抛物线交于点D、E两点(点D在对称轴的左侧).过点D、E分别作x轴的垂线,垂足分别为G、F,当矩形DEFG中DE=2DG时,求D点的坐标. -
科目: 来源: 题型:
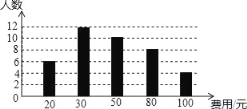
查看答案和解析>>【题目】在全民读书月活动中,某校随机调查了40名同学,本学期计划购买课外书的费用情况,并将结果绘制成如图所示的统计图.根据相关信息,解答下列问题,直接写出结果.
(1)这次调查获取的样本数据的众数是 .
(2)这次调查获取的样本数据的中位数是 .
(3)若该校共有1200名学生,根据样本数据,估计本学期计划购买课外书花费50元的学生有 人.
相关试题

