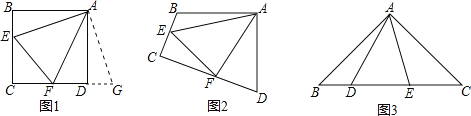
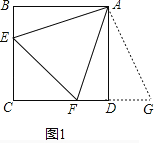
【题目】(1)探究:如图1和2,四边形ABCD中,已知AB=AD,∠BAD=90°,点E、F分别在BC、CD上,∠EAF=45°.
①如图1,若∠B、∠ADC都是直角,把△ABE绕点A逆时针旋转90°至△ADG,使AB与AD重合,则能证得EF=BE+DF,请写出推理过程;
②如图2,若∠B、∠D都不是直角,则当∠B与∠D满足数量关系 时,仍有EF=BE+DF;
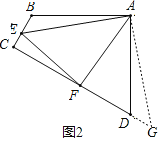
(2)拓展:如图3,在△ABC中,∠BAC=90°,AB=AC=2![]() ,点D、E均在边BC上,且∠DAE=45°.若BD=1,求DE的长.
,点D、E均在边BC上,且∠DAE=45°.若BD=1,求DE的长.
参考答案:
【答案】(1)①理由详见解析;②∠B+∠ADC=180°;(2)![]() .
.
【解析】
试题分析:(1)①把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,证出△AFG≌△AFE,根据全等三角形的性质得出EF=FG,即可得出答案;
②把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,证出△AFE≌△AFG,根据全等三角形的性质得出EF=FG,即可得出答案;
(2)把△ACE旋转到ABF的位置,连接DF,证明△AFE≌△AFG(SAS),则EF=FG,∠C=∠ABF=45°,△BDF是直角三角形,根据勾股定理得到BD2+CE2=DE2
,由∠BAC=90°,AB=AC=2![]() ,知BC=4,所以DC=3,EC=3﹣DE,代入解方程即可.
,知BC=4,所以DC=3,EC=3﹣DE,代入解方程即可.
试题解析:解:(1)①理由是:如图1,
∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,如图1,
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线,
则∠DAG=∠BAE,AE=AG,
∠FAG=∠FAD+∠GAD=∠FAD+∠BAE=90°﹣45°=45°=∠EAF,
即∠EAF=∠FAG,
在△EAF和△GAF中,AF=AF,∠EAF=∠FAG,AE=AG,
∴△AFG≌△AFE(SAS),
∴EF=FG=BE+DF;
②当∠B+∠ADC=180°时,EF=BE+DF;
∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,如图2,
∴∠BAE=∠DAG,
∵∠BAD=90°,∠EAF=45°,
∴∠BAE+∠DAF=45°,
∴∠EAF=∠FAG,
∵∠ADC+∠B=180°,
∴∠FDG=180°,点F、D、G共线,
在△AFE和△AFG中,AF=AF,∠EAF=∠FAG,AE=AG,
∴△AFE≌△AFG(SAS),
∴EF=FG,
即:EF=BE+DF,
故答案为:∠B+∠ADC=180°;
(2)把△ACE旋转到ABF的位置,连接DF,则∠FAB=∠CAE.
∵∠BAC=90°,∠DAE=45°,
∴∠BAD+∠CAE=45°,
又∵∠FAB=∠CAE,
∴∠FAD=∠DAE=45°,
则在△ADF和△ADE中,AD=AD,∠FAD=∠DAE,AF=AE,
∴△ADF≌△ADE,
∴DF=DE,∠C=∠ABF=45°,
∴∠BDF=90°,
∴△BDF是直角三角形
∴BD2+BF2=DF2,
∴BD2+CE2=DE2.
∵∠BAC=90°,AB=AC=2![]() ,
,
∴BC=4,
∵BD=1,
∴DC=3,EC=3﹣DE,
∴1+(3﹣DE)2=DE2,
解得:DE=![]() .
.
-
科目: 来源: 题型:
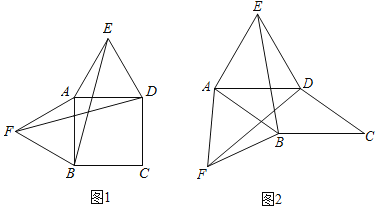
查看答案和解析>>【题目】如图,以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,连接BE、DF.
(1)当四边形ABCD为正方形时(如图1),则线段BE与DF的数量关系是 .
(2)当四边形ABCD为平行四边形时(如图2),问(1)中的结论是否还成立?若成立,请证明;若不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,如果 x 与 y 都是整数,就称点(x,y)为整点.下列命题中错误的是( )
A. 存在这样的直线,既不与坐标轴平行,又不经过任何整点
B. 若 k 与 b 都是无理数,则直线 y=kx+b 不经过任何整点
C. 若直线 y=kx+b 经过无数多个整点,则 k 与 b 都是有理数
D. 存在恰好经过一个整点的直线
-
科目: 来源: 题型:
查看答案和解析>>【题目】张浩调查统计了他们家5月份每次打电话的通话时长,并将统计结果进行分组(每组含量最小值,不含最大值),将分组后的结果绘制成如图所示的频数分布直方图,则下列说法中不正确的是( )

A. 张浩家5月份打电话的总频数为80次
B. 张浩家5月份每次打电话的通话时长在5﹣10分钟的频数为15次
C. 张浩家5月份每次打电话的通话时长在10﹣15分钟的频数最多
D. 张浩家5月份每次打电话的通话时长在20﹣25分钟的频率为6%
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,已知AB=CD,M、N、P分别是AD、BC、BD的中点∠ABD=20°,∠BDC=70°,则∠NMP的度数为( )

A. 50° B. 25° C. 15° D. 20
-
科目: 来源: 题型:
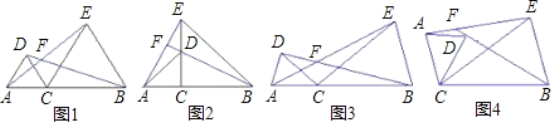
查看答案和解析>>【题目】已知点C为线段AB上一点,分别以AC、BC为边在线段AB的同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,直线AE与BD交于点F.
(1)如图1,若∠ACD=60°,则∠AFB=______,如图2,若∠ACD=90°,则∠AFB=______,如图3,若∠ACD=α,则∠AFB=______(用含α的式子表示);
(2)设∠ACD=α,将图3中的△ACD绕点C顺时针旋转任意角度(交点F至少在BD、AE中的一条线段上),如图4,试探究∠AFB与α的数量关系,并予以说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种运算:
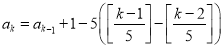 ,其中k是正整数,且k ≥2,[x]表示非负实数x的整数部分,例如[2.6]=2,[0.8]=0.若
,其中k是正整数,且k ≥2,[x]表示非负实数x的整数部分,例如[2.6]=2,[0.8]=0.若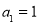 ,则
,则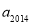 的值为( )
的值为( )A.2015B.4C.2014D.5
相关试题

